链式表示与实现
链式表示与实现
链表
线性表链式存储结构的特点是:用一组任意的存储单元存储线性表的数据元素(这组存储单元可以是连续的,也可以是不连续的)。
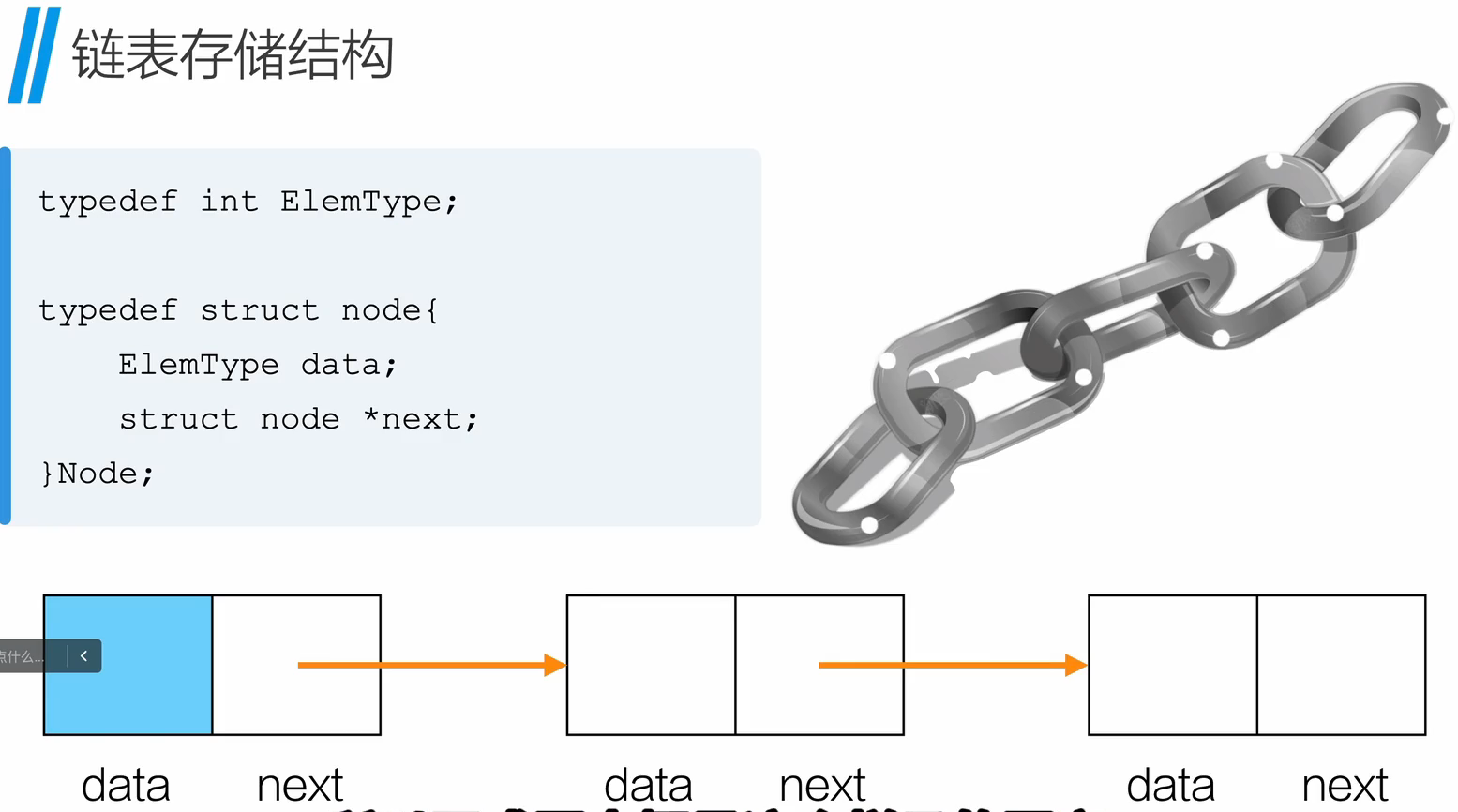
为了表示每个数据元素 a_i 与其直接后继数据元素 a_{i+1} 之间的逻辑关系,对数据元素 a_i 来说,除了其本身的信息之外,还需要存储一个指示其直接后继的信息(直接后继的存储位置)。这两部分信息组成数据元素 a_i 的存储映像,称为节点(node)。
结点包括两个域:其中存储数据元素信息的称为 数据域 ;存储直接后继存储位置有域称为 指针域 。指针域中存储的信息称作指针或链。
n个结点[ a_i(1≤i≤n) 的存储映像] 链接成一个链表,即为线性表(a1,a2,…an)
1
2
3
4
5
6
| typedef int ElemType;
typedef struct node{
ElemType data;
struct node * next;
}Node;
|
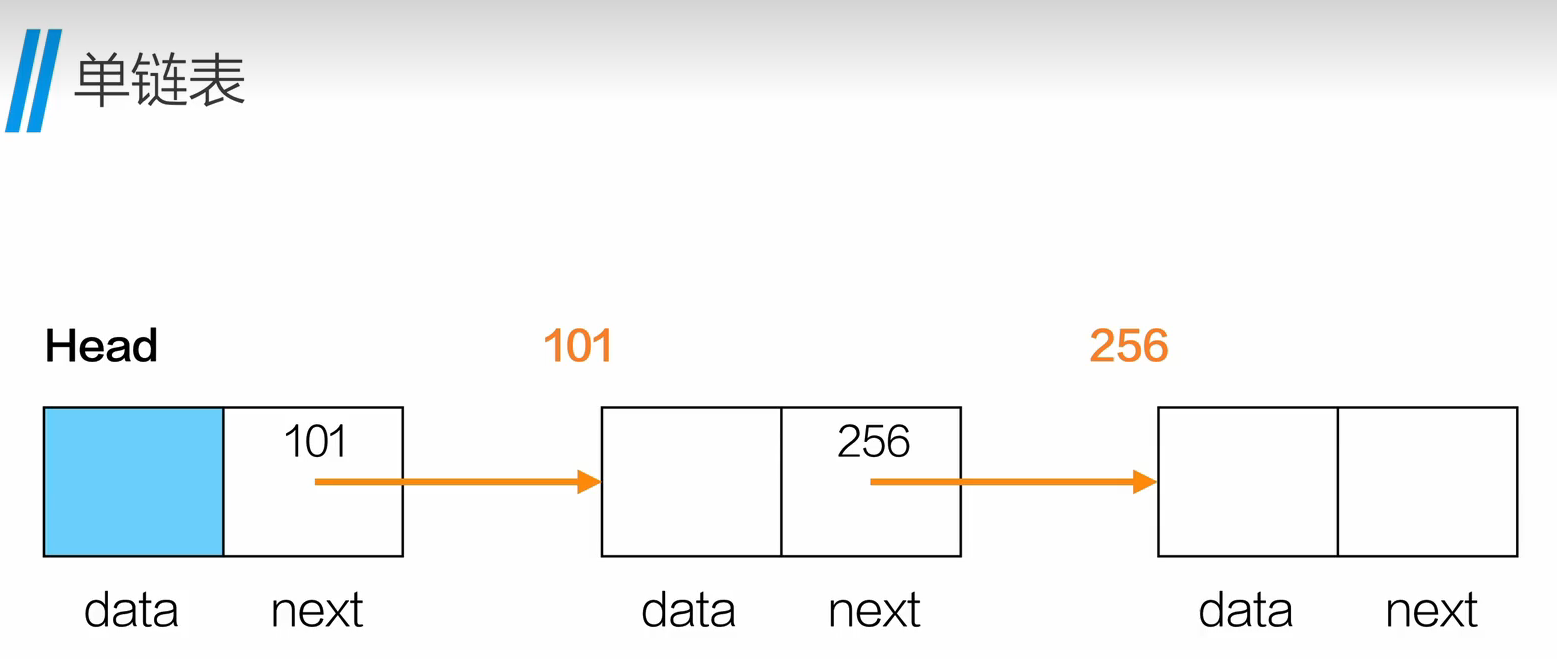
一、单链表
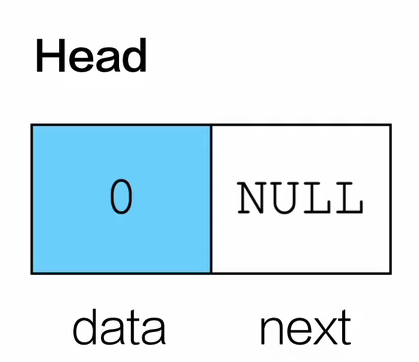
初始化
1
2
3
4
5
6
7
8
9
10
11
12
| Node * InitList(){
Node * link = (Node *)malloc(sizeof(Node));
link->data = 0;
link->next = NULL;
return link;
}
int main(int argc, char const *argv[])
{
Node * list = InitList();
return 0;
}
|
插入数据
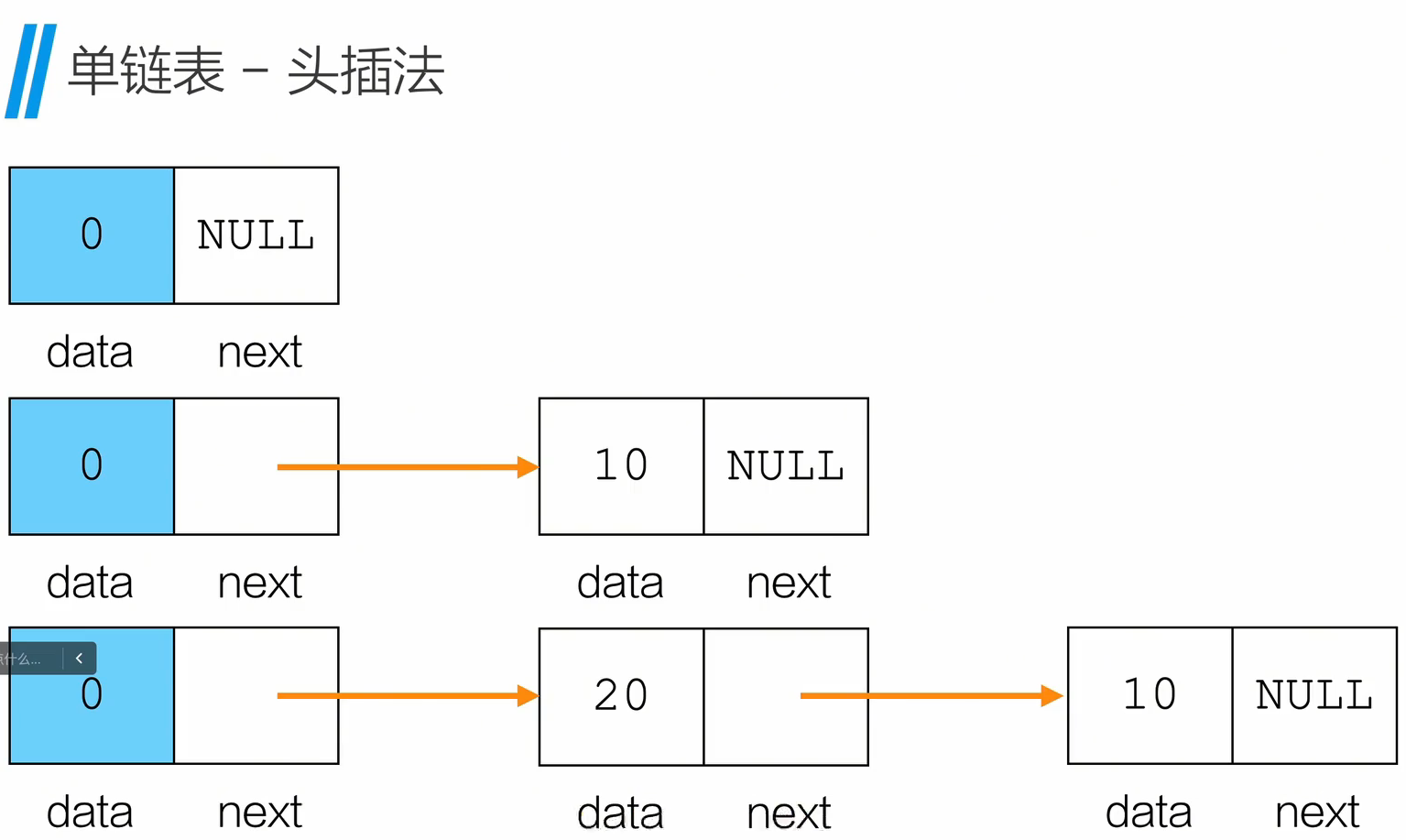
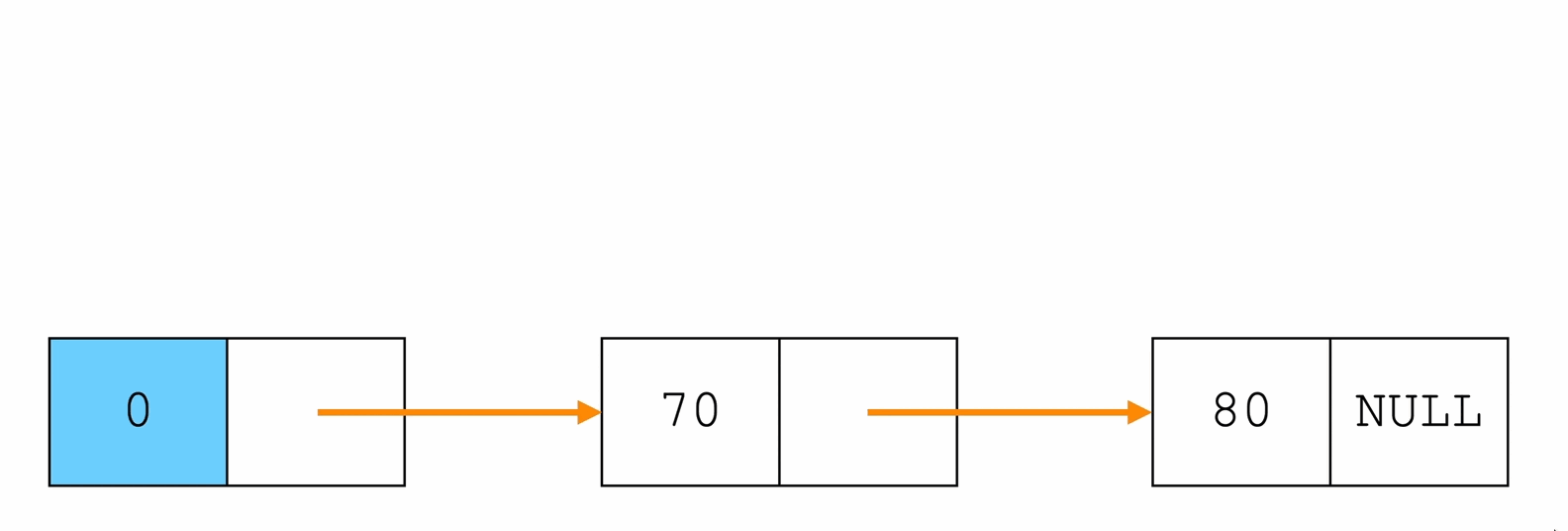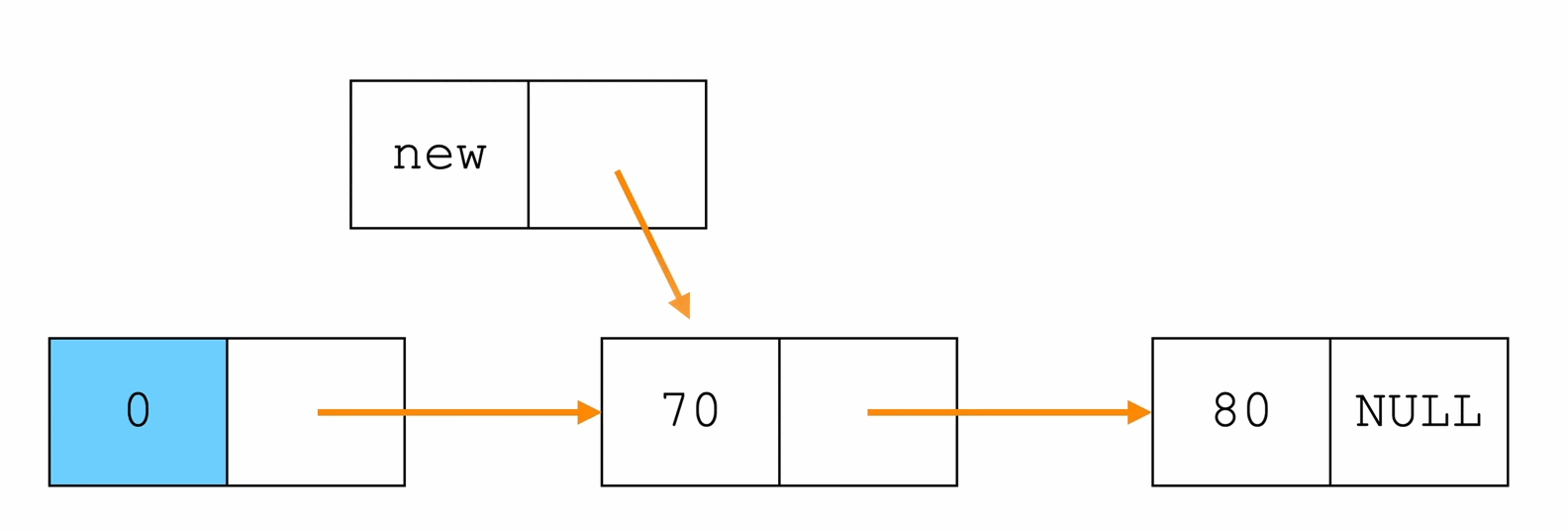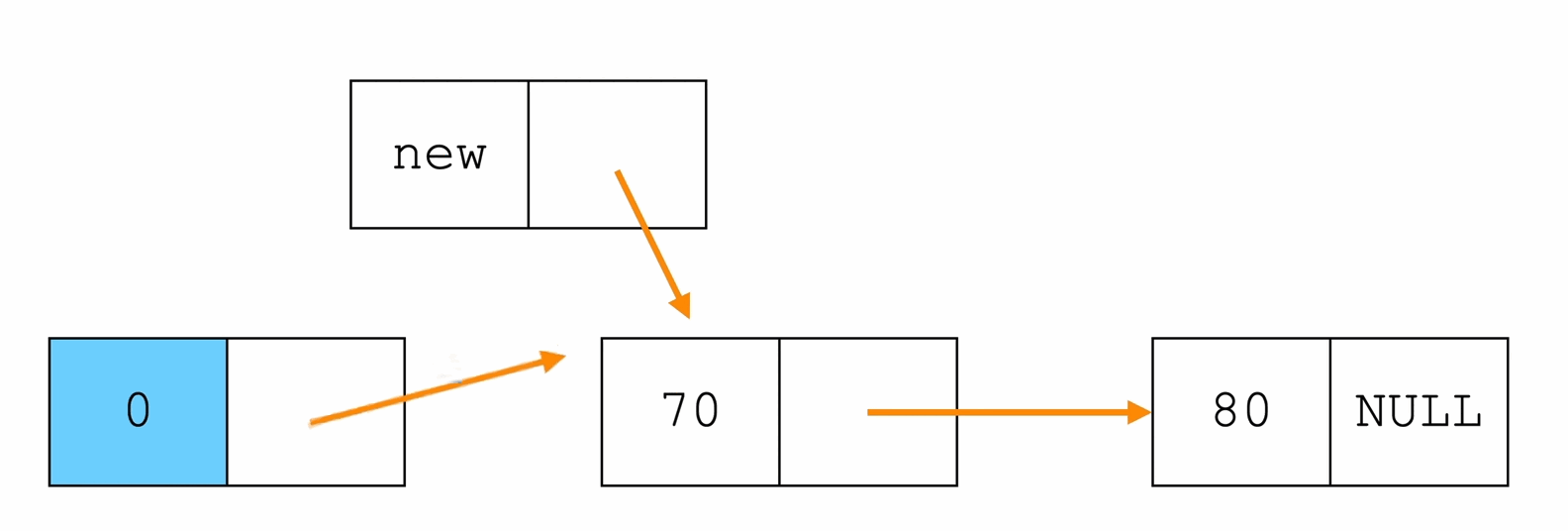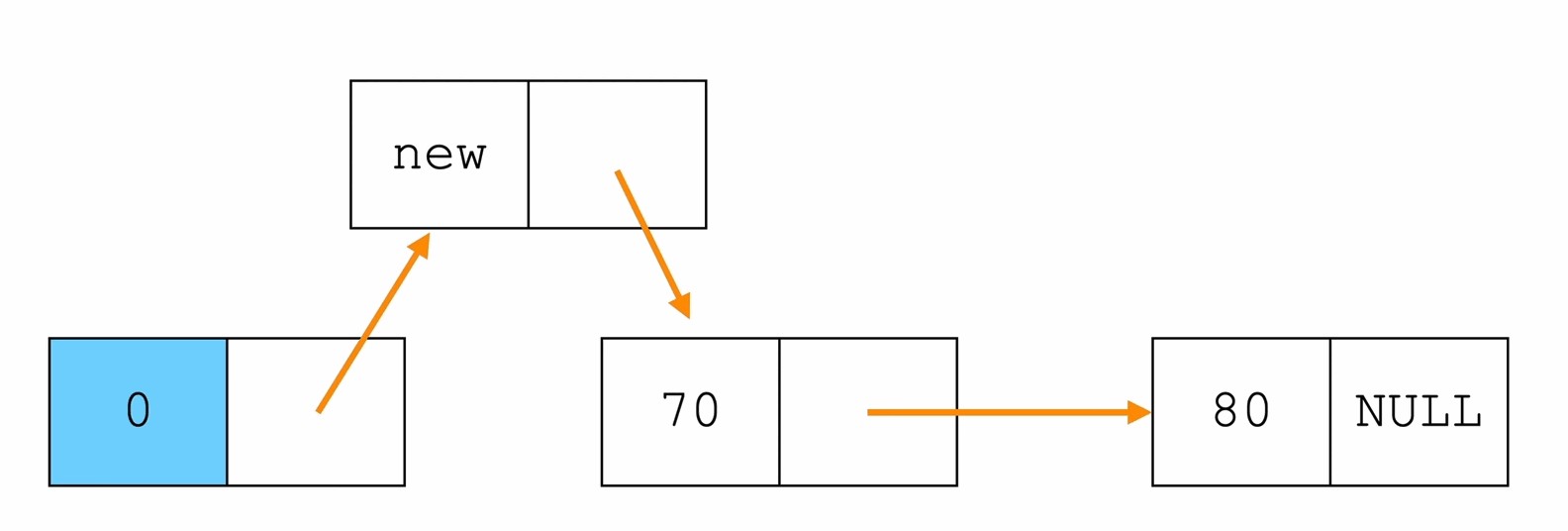
头插法
每一次插入数据都插入到头结点的后面
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| int insertHead(Node * L, ElemType e){
Node * p = (Node *)malloc(sizeof(Node));
p->data = e;
p->next = L->next;
L->next = p;
return 1;
}
int main(int argc, char const *argv[])
{
Node * list = InitList();
insertHead(list,10);
insertHead(list,20);
insertHead(list,30);
printlistNode(list);
return 0;
}
|
尾插法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
Node * get_tail(Node * L){
Node * p = L;
while(p->next != NULL){
p = p->next;
}
return p;
}
Node * insertTail(Node * tail, ElemType e){
Node * p = (Node *)malloc(sizeof(Node));
p->data = e;
tail->next = p;
p->next = NULL;
return p;
}
int main(int argc, char const *argv[])
{
Node * list = InitList();
Node * tail = get_tail(list);
tail = insertTail(tail,10);
tail = insertTail(tail,20);
tail = insertTail(tail,30);
printlistNode(list);
return 0;
}
|
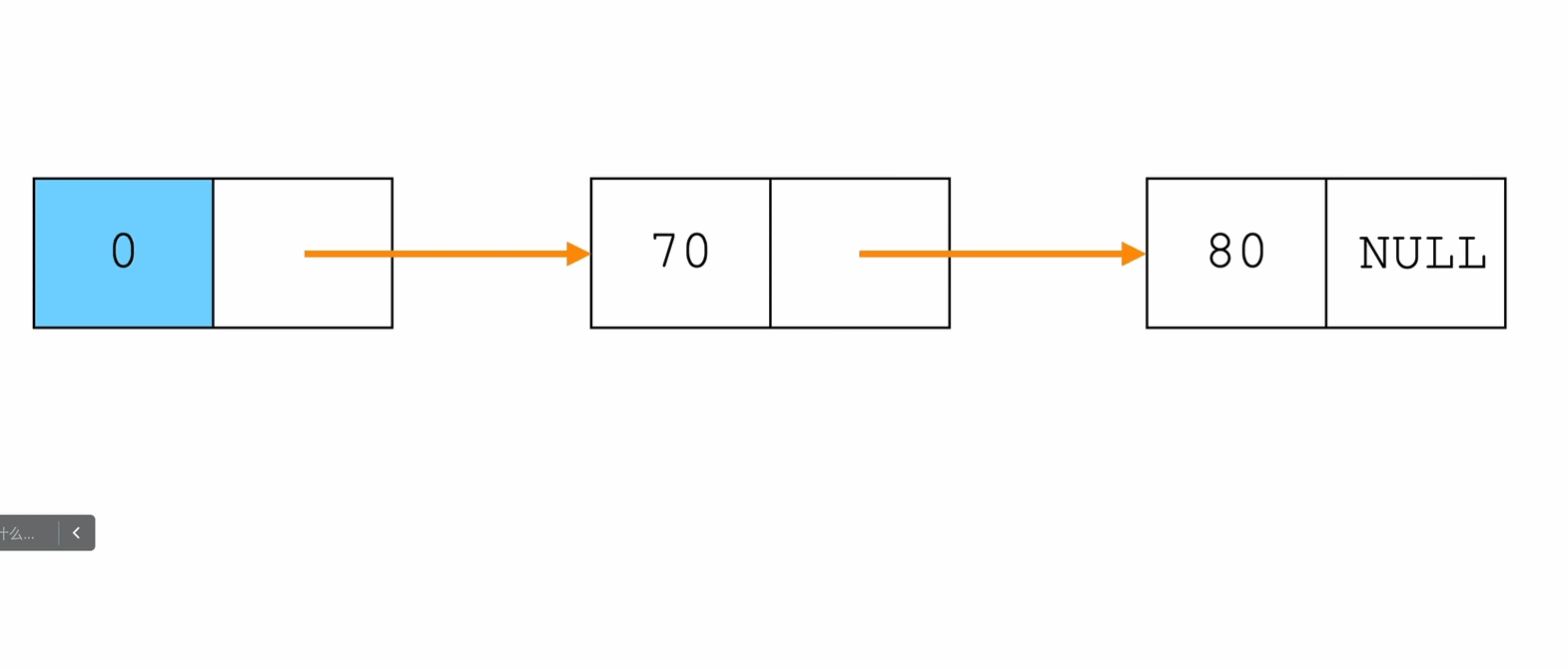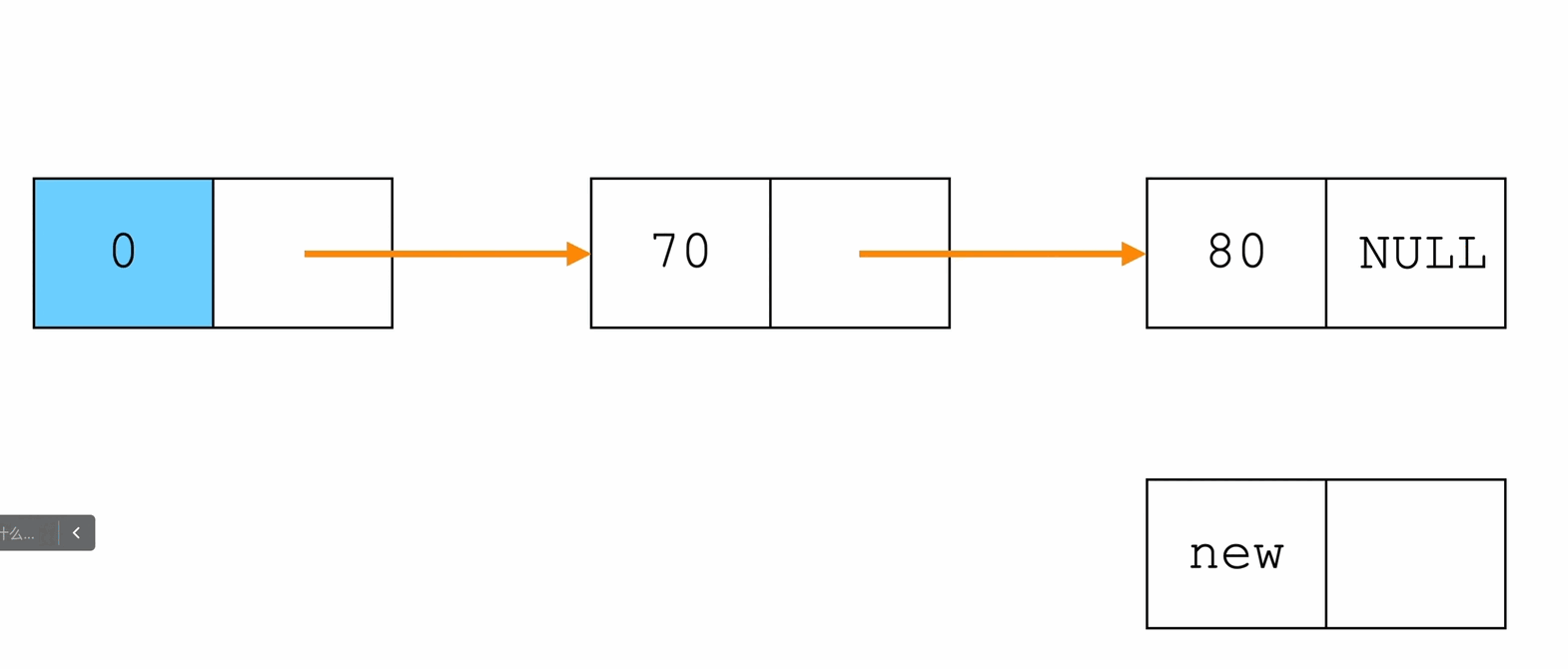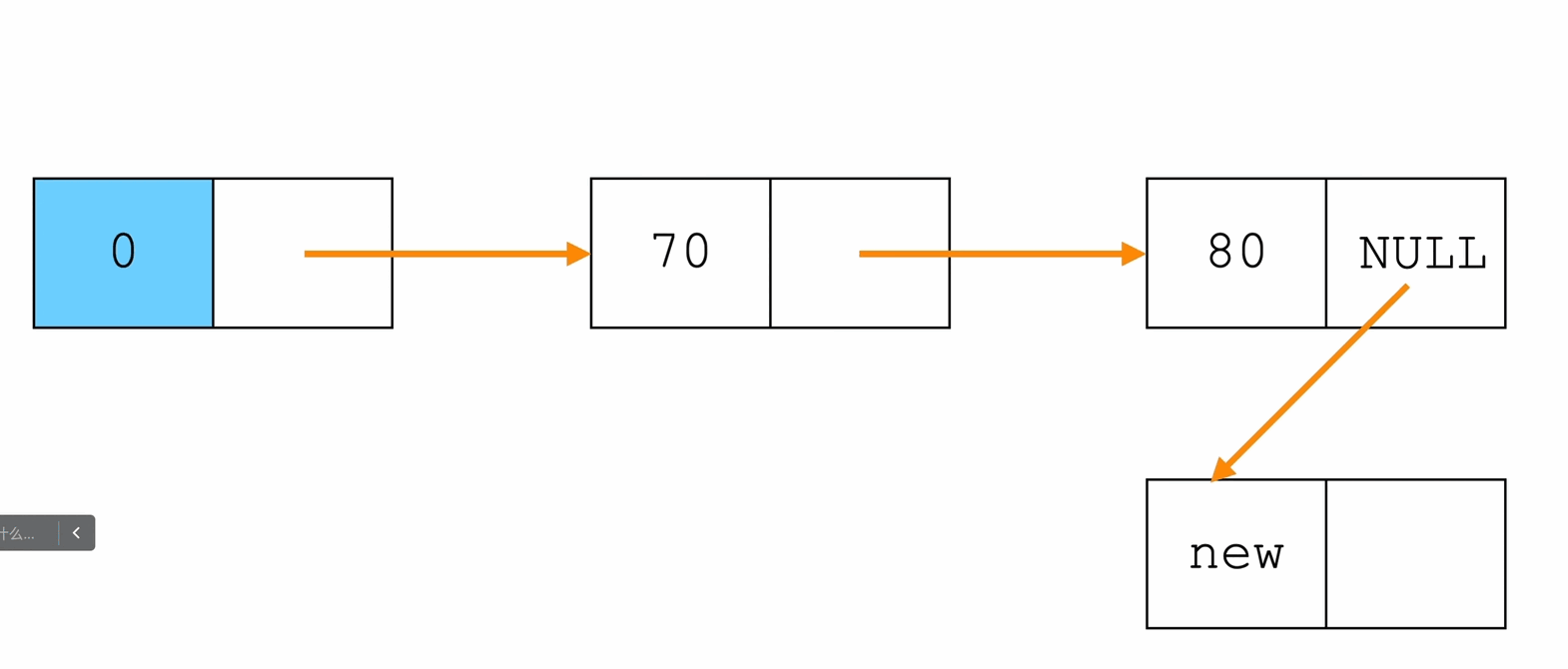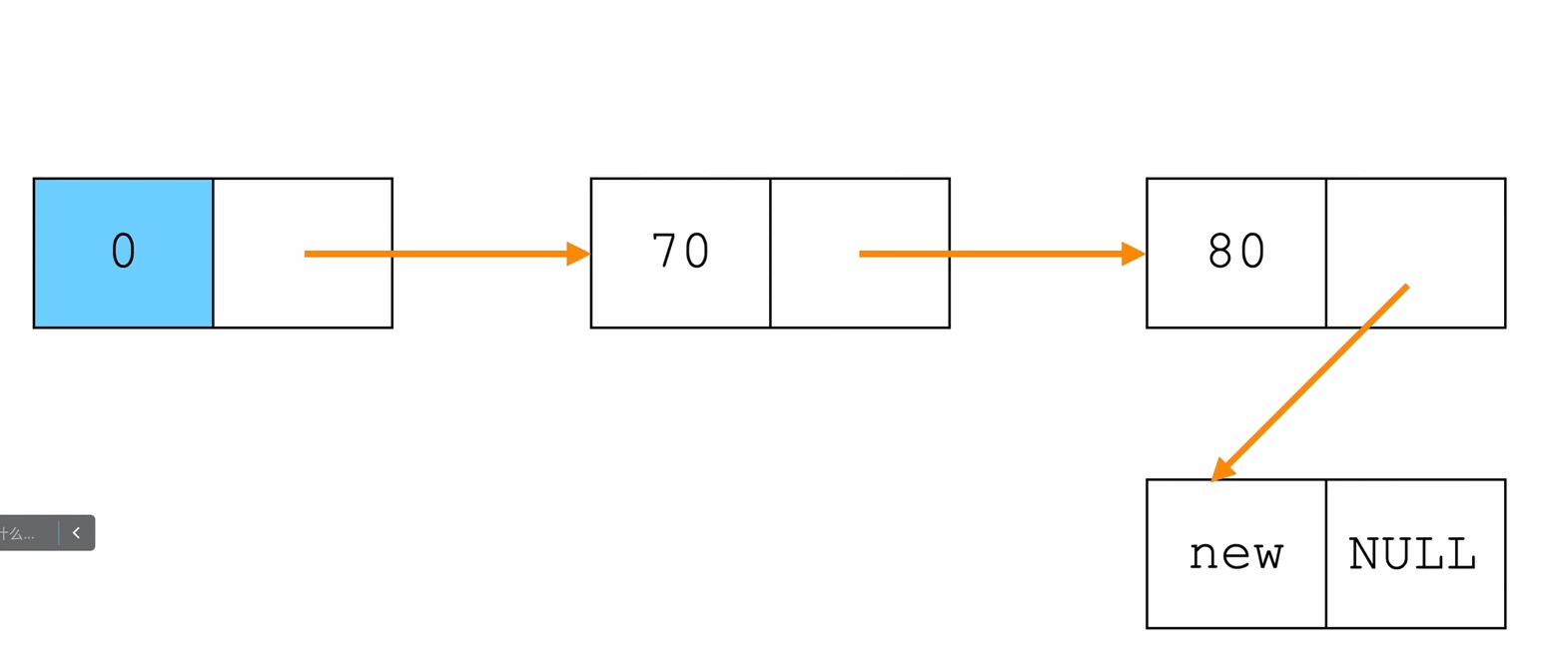
在指定位置插入
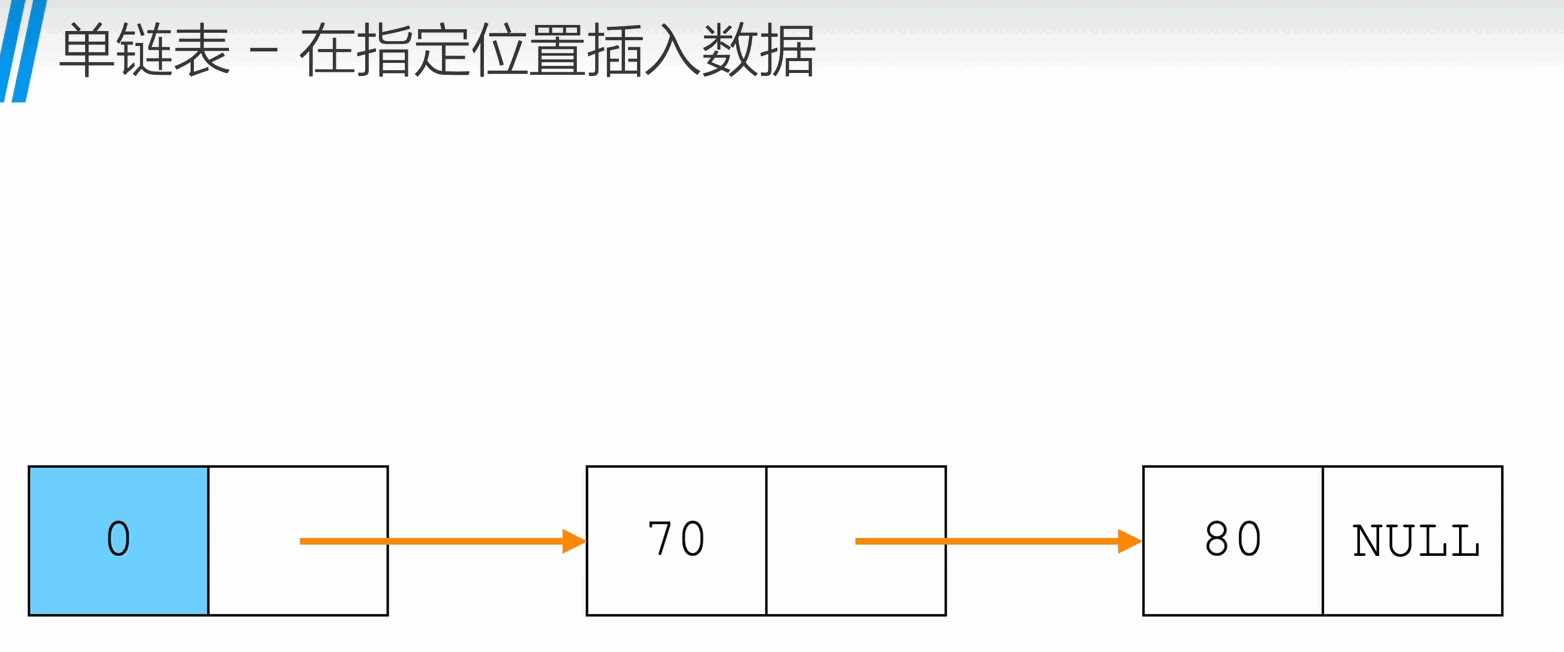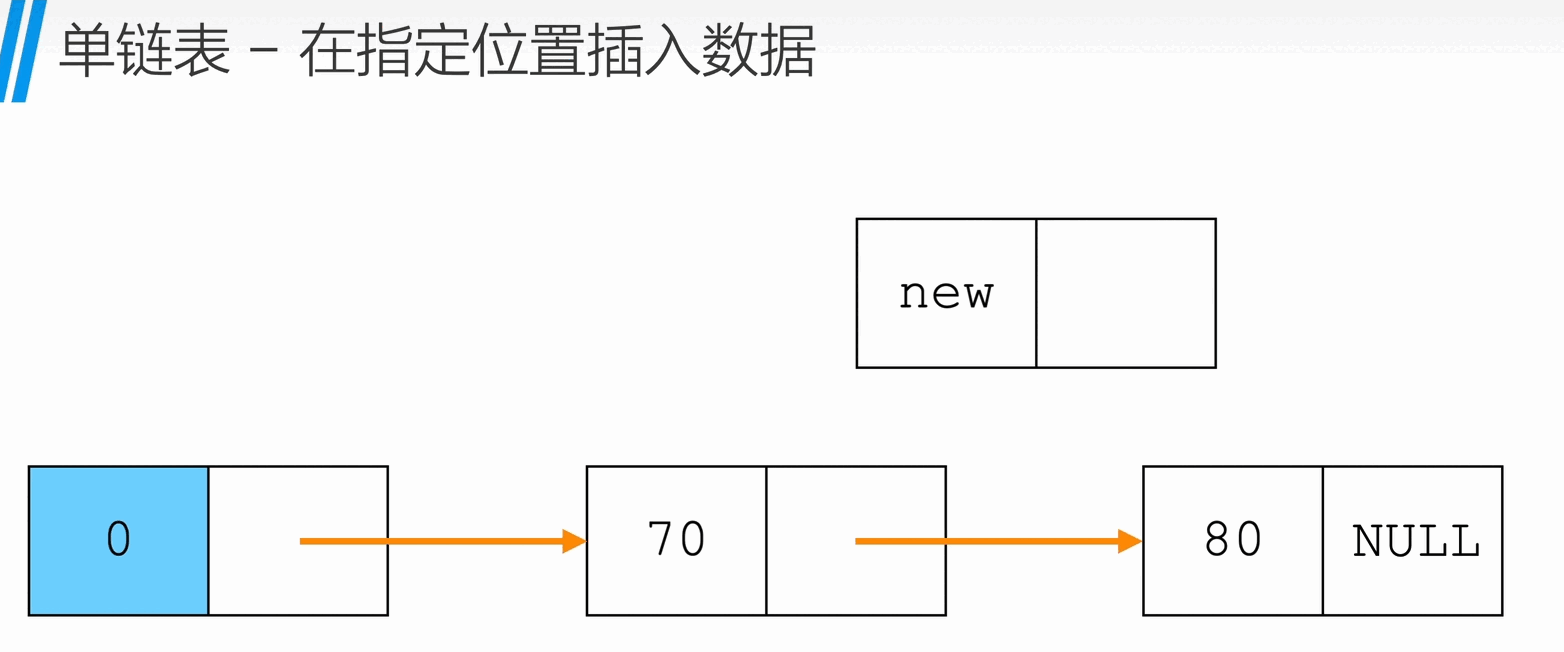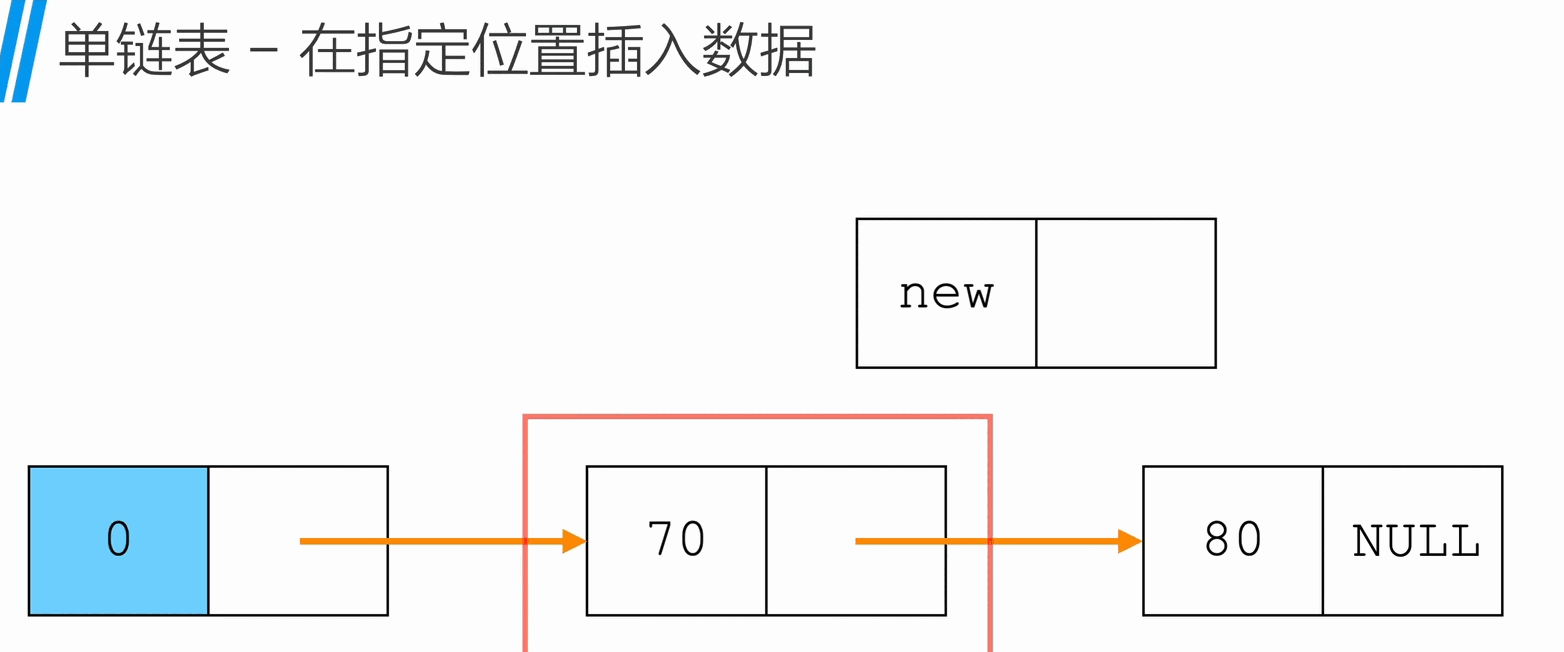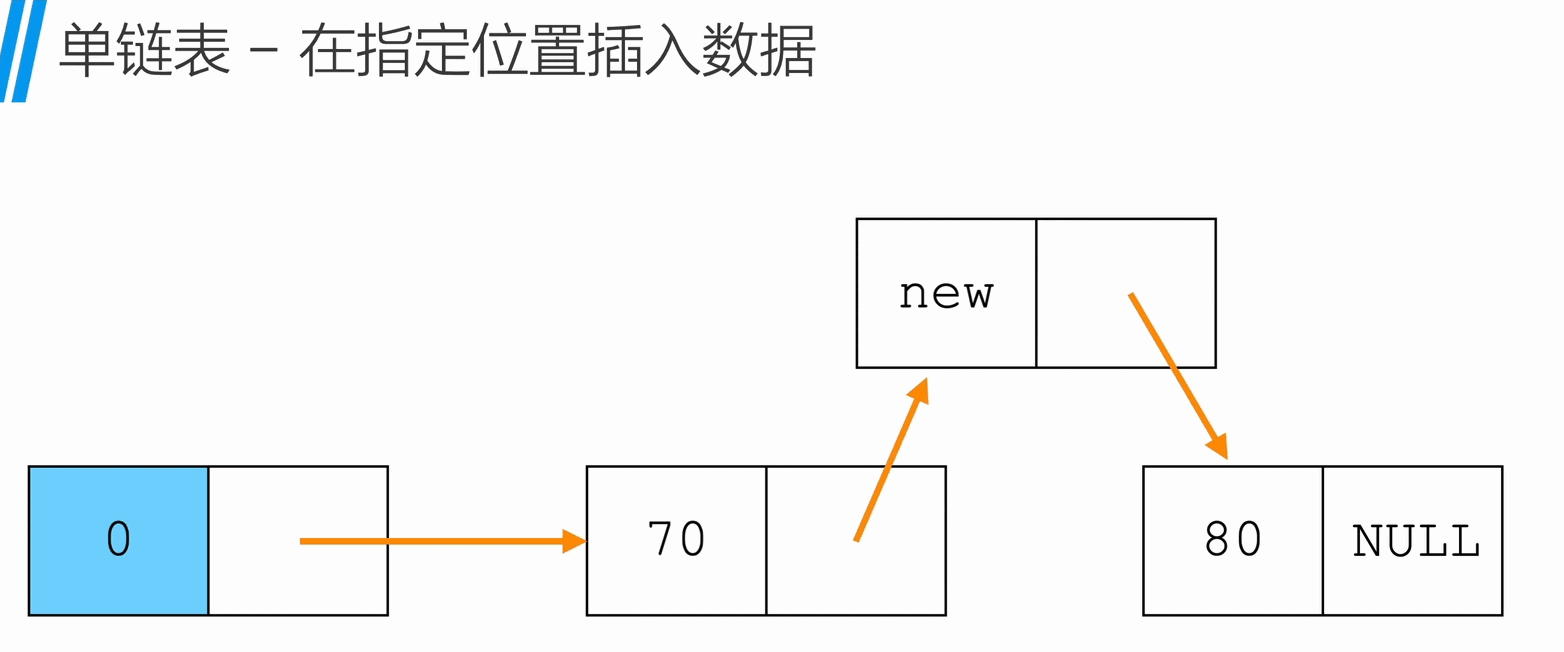
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
int insertNode(Node * L, int index, ElemType e){
Node * p = L;
int i = 0;
while(i < index - 1){
p = p->next;
i++;
if(p == NULL){
return 0;
}
}
Node * q = (Node *)malloc(sizeof(Node));
q->data = e;
q->next = p->next;
p->next = q;
return 1;
}
|
遍历
1
2
3
4
5
6
7
8
| void printlistNode(Node * L){
Node * p = L->next;
while(p != NULL){
printf("%d -> ", p->data);
p = p->next;
}
printf("NULL\n");
}
|
头插法的顺序和排列的顺序是相反的
删除节点
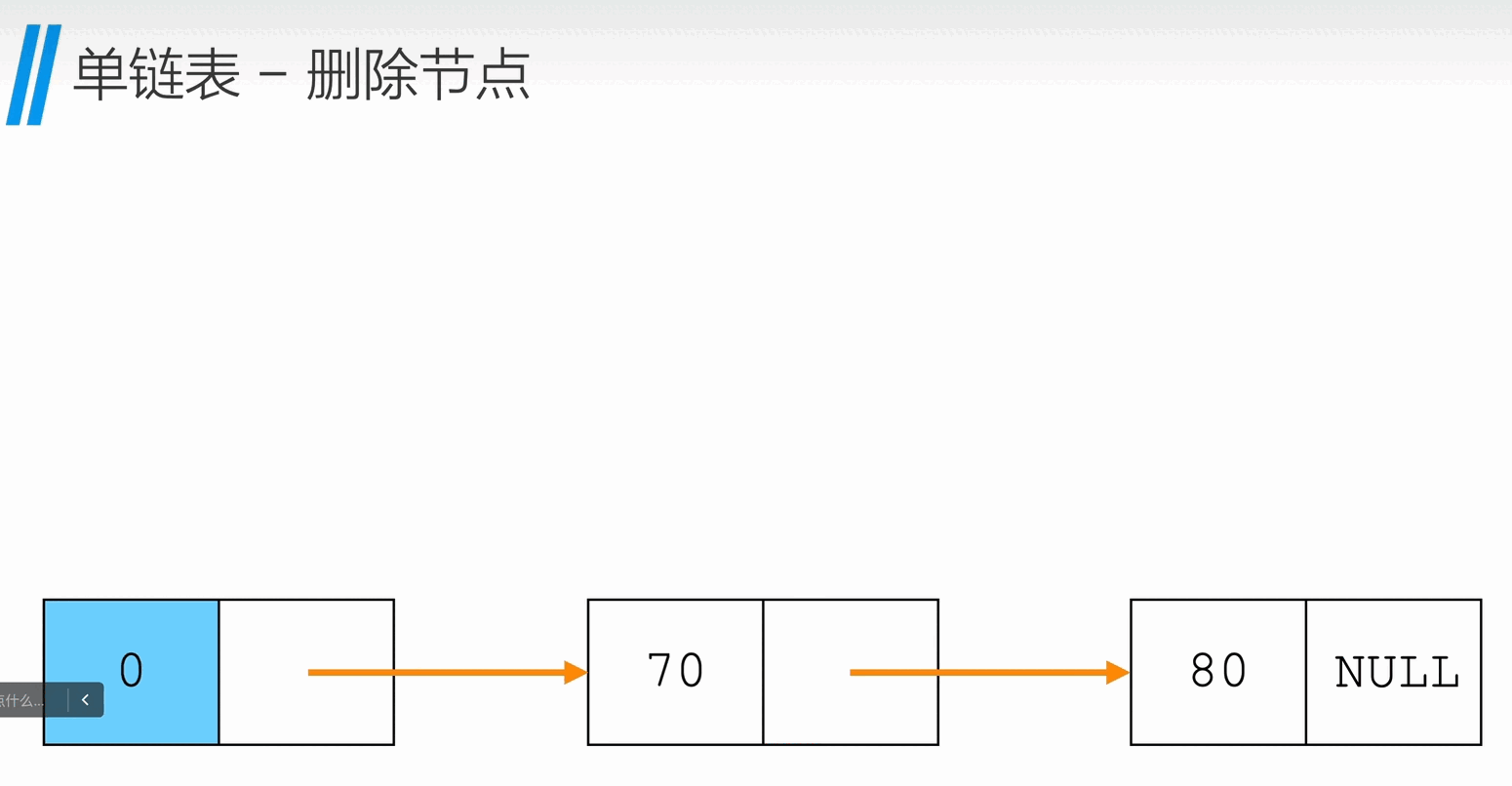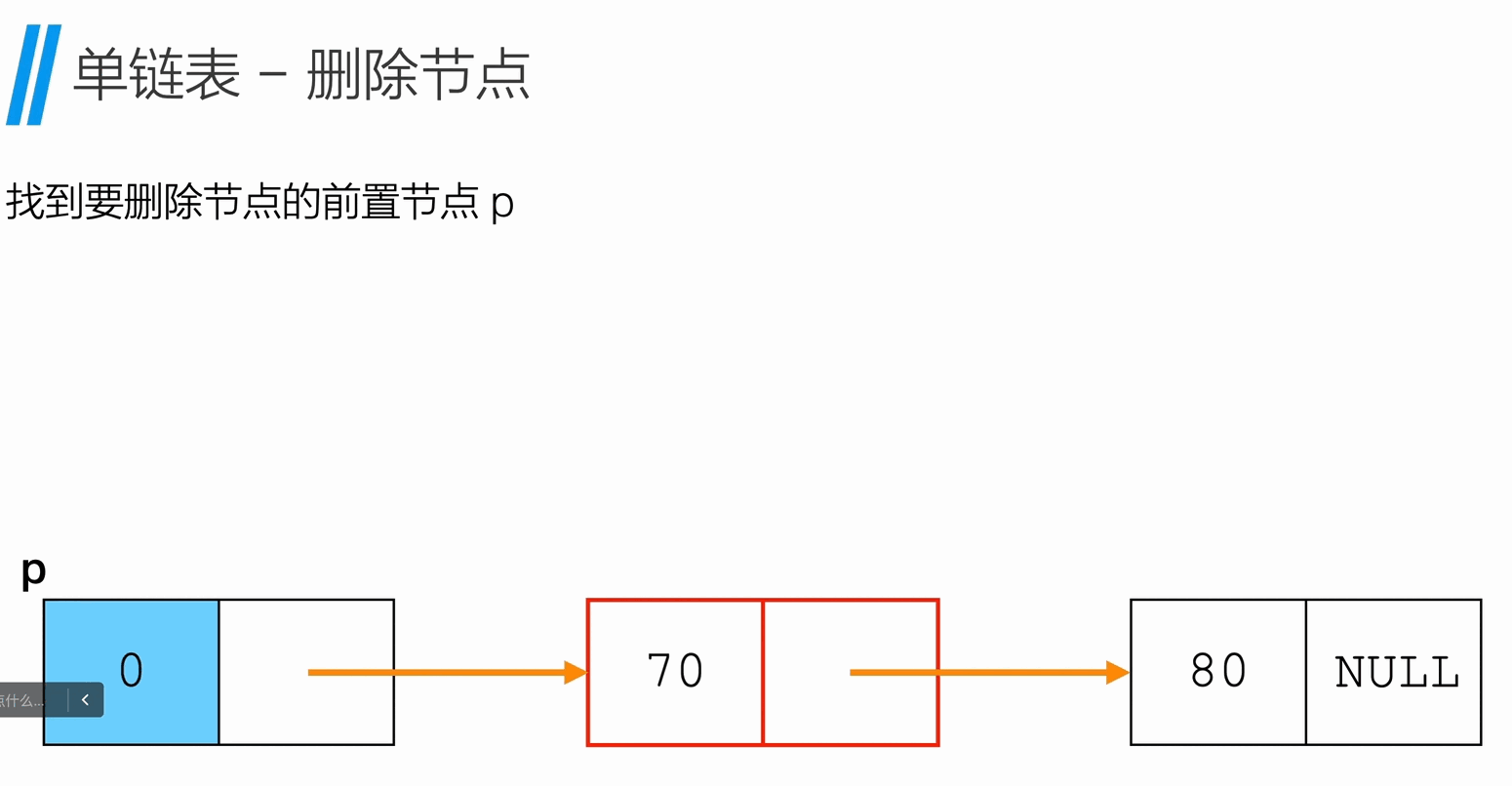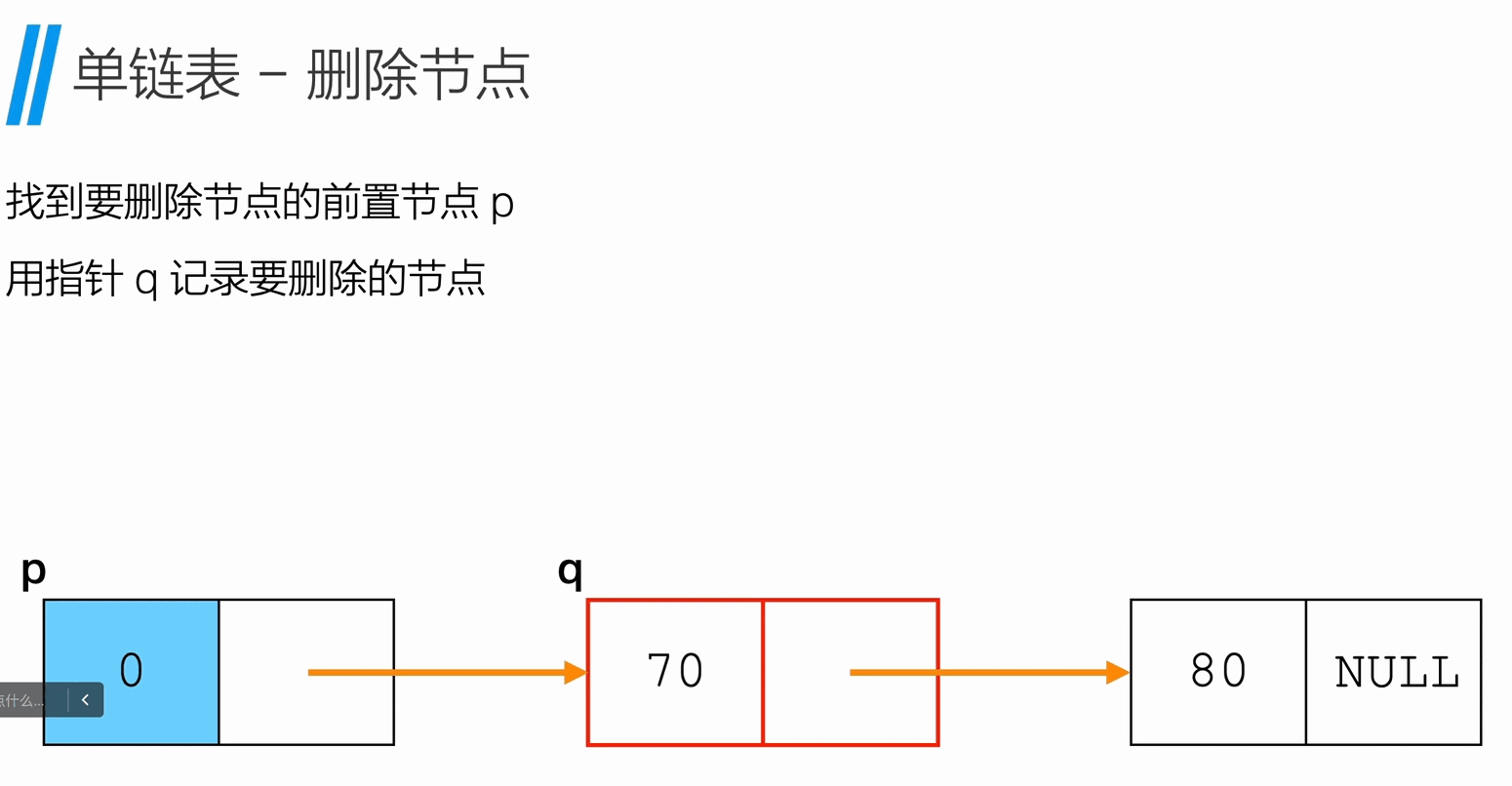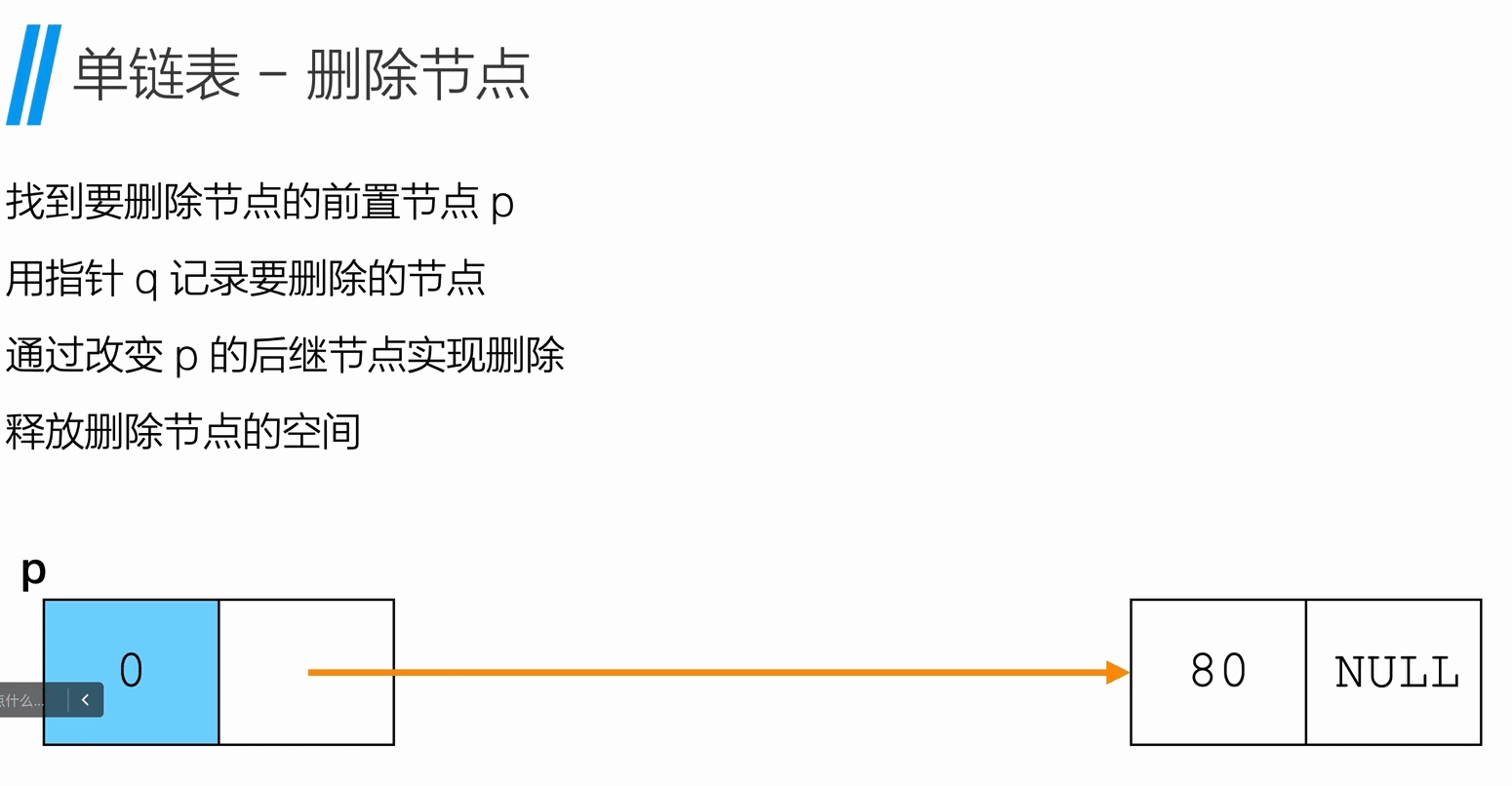
获取链表长度
1
2
3
4
5
6
7
8
9
10
|
int listLength(Node * L){
Node * p = L;
int len = 0;
while(p != NULL){
p = p->next;
len++;
}
return len;
}
|
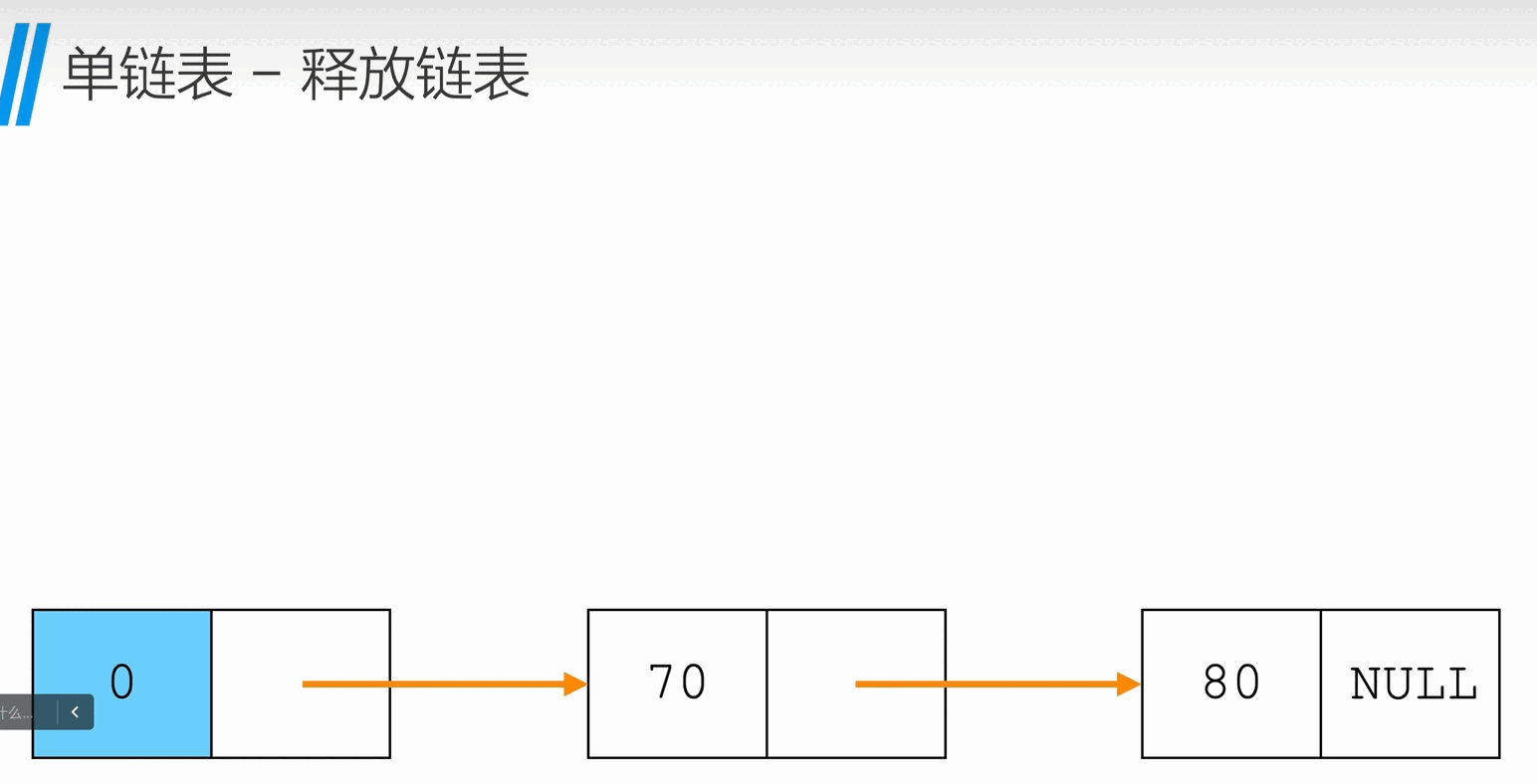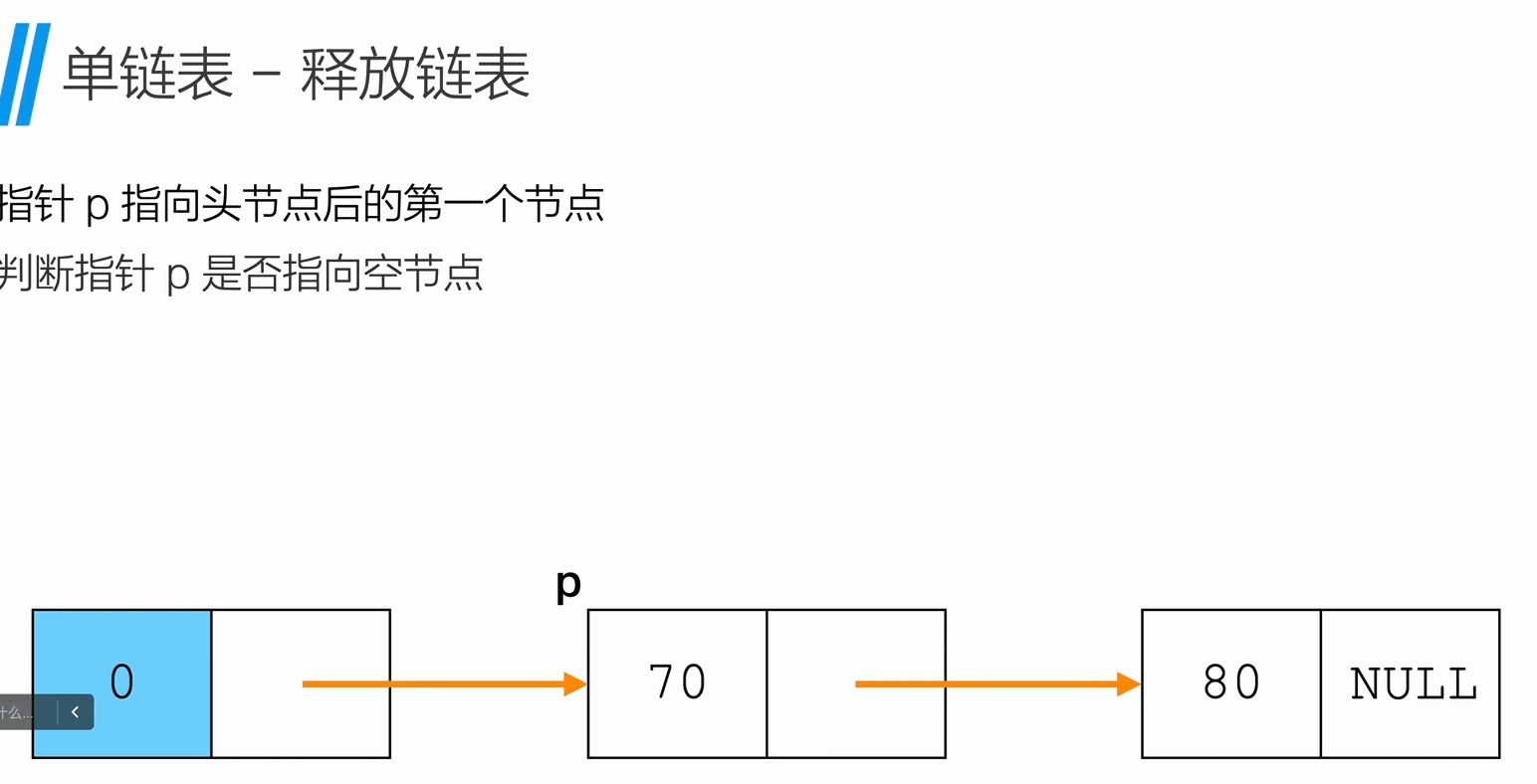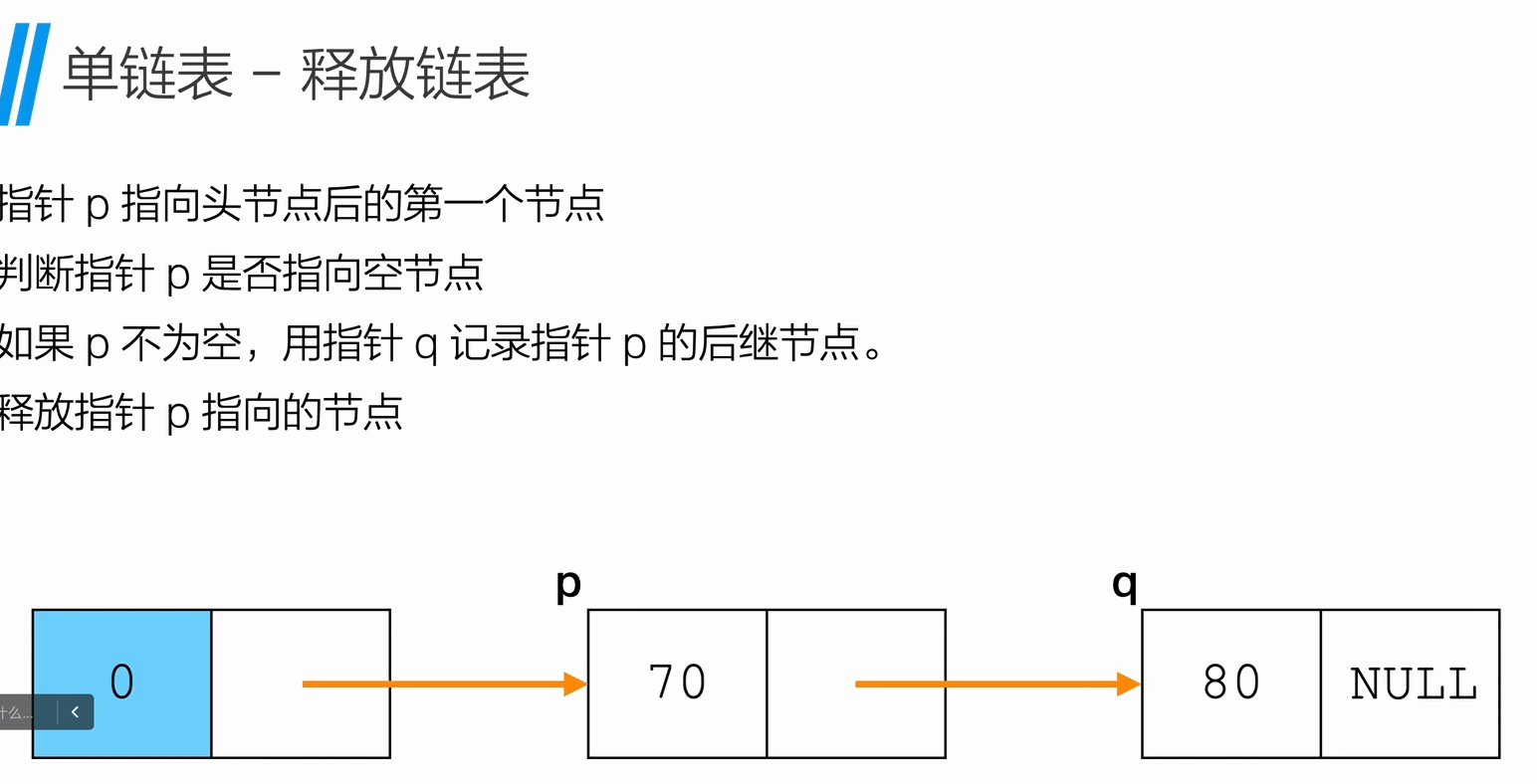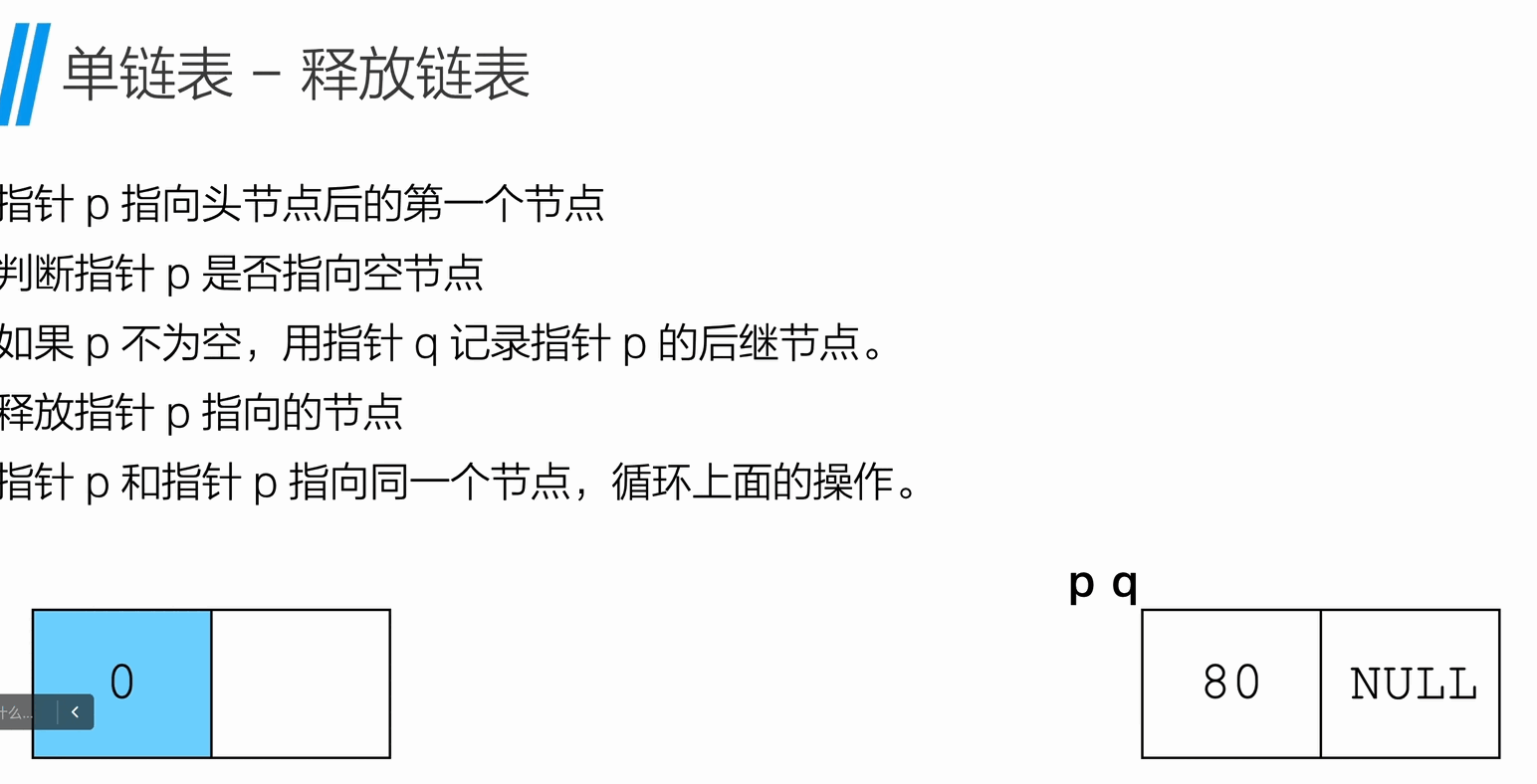
释放链表
1
2
3
4
5
6
7
8
9
10
11
12
|
void freeList(Node * L){
Node * p = L->next;
Node * q;
while(p !=NULL){
q = p->next;
free(p);
p = q;
}
L->next = NULL;
}
|
问题
单链表局限性?
不容易找到前驱节点
二、循环链表

判断链表是否有环
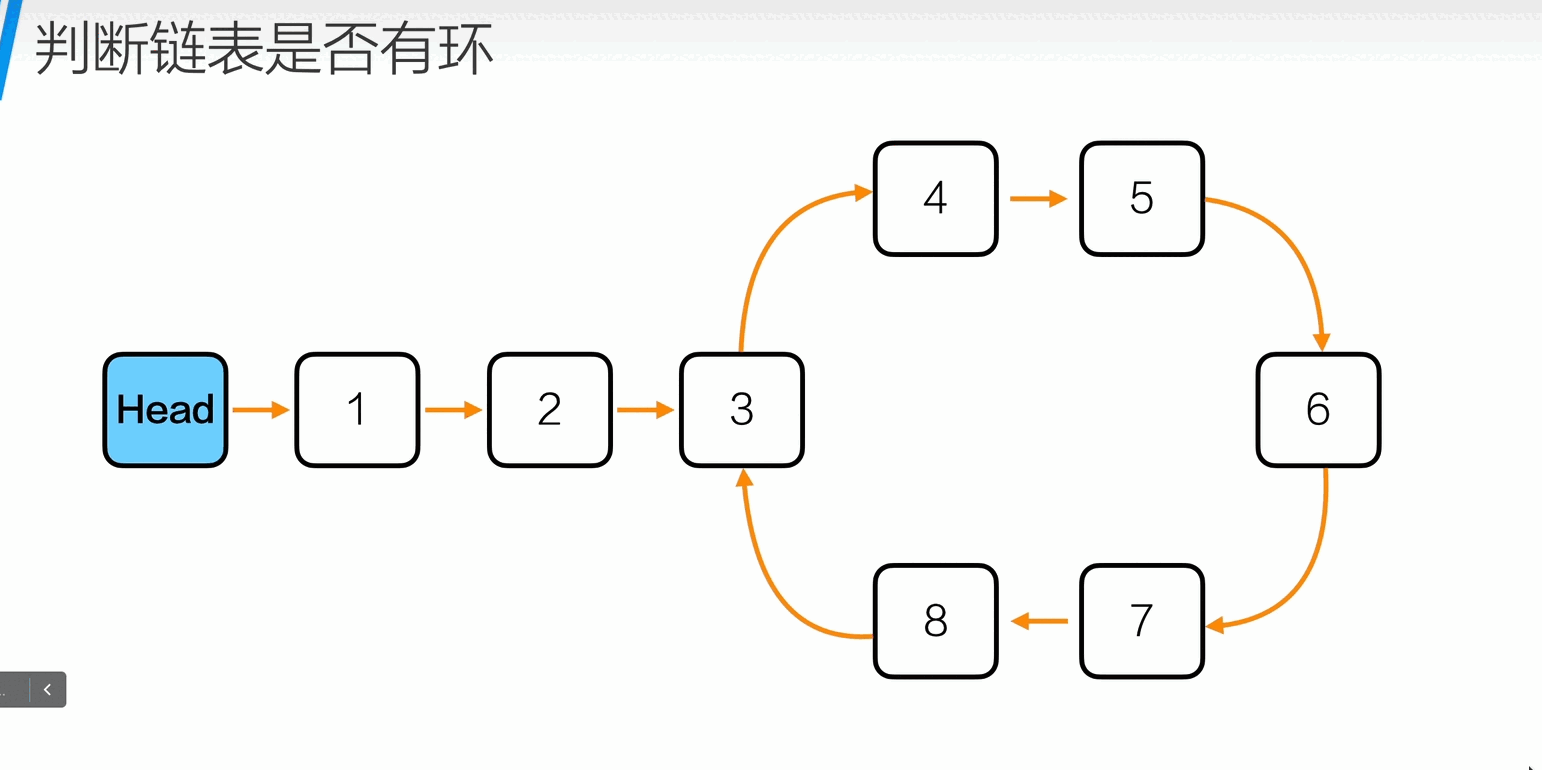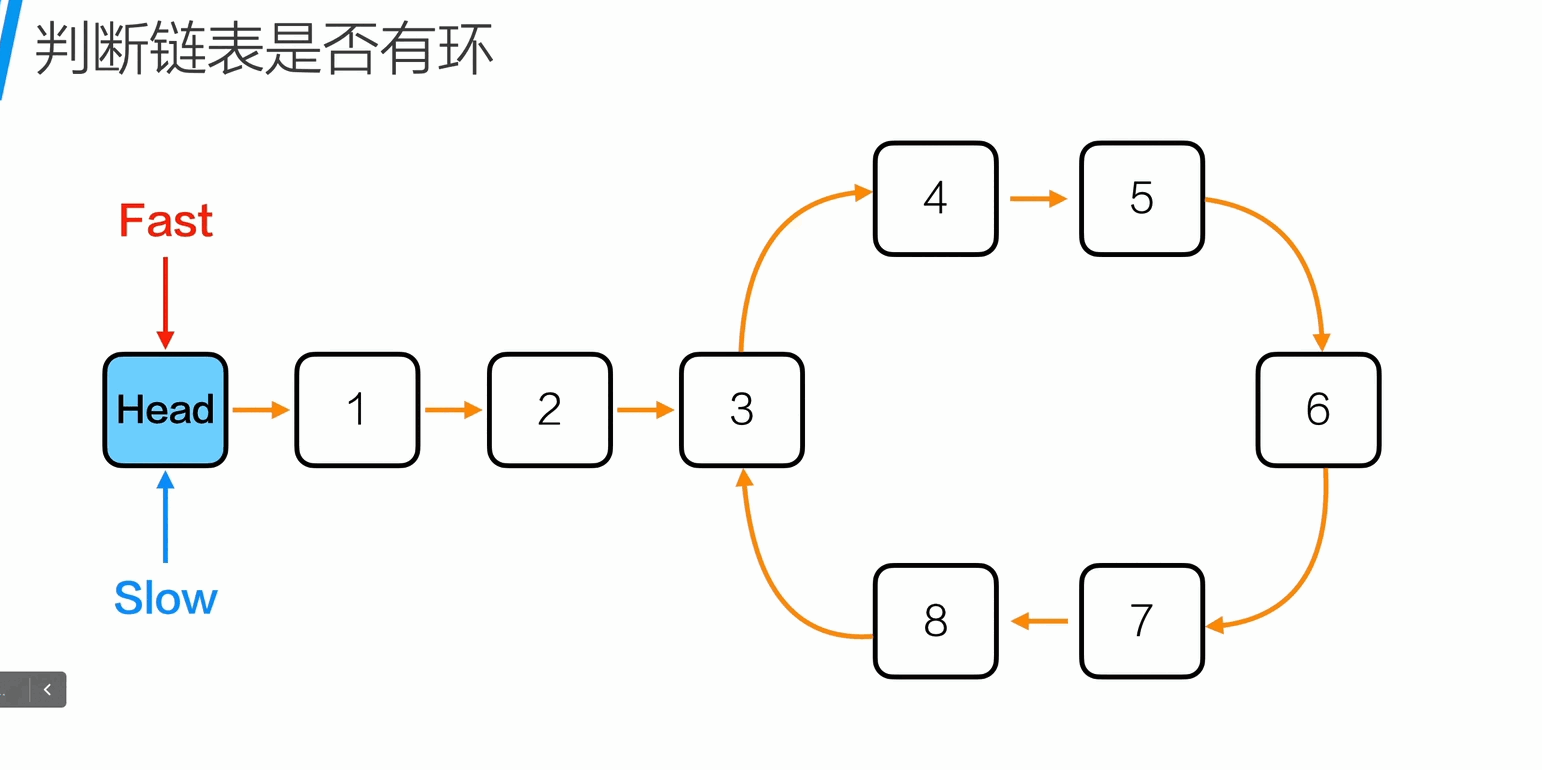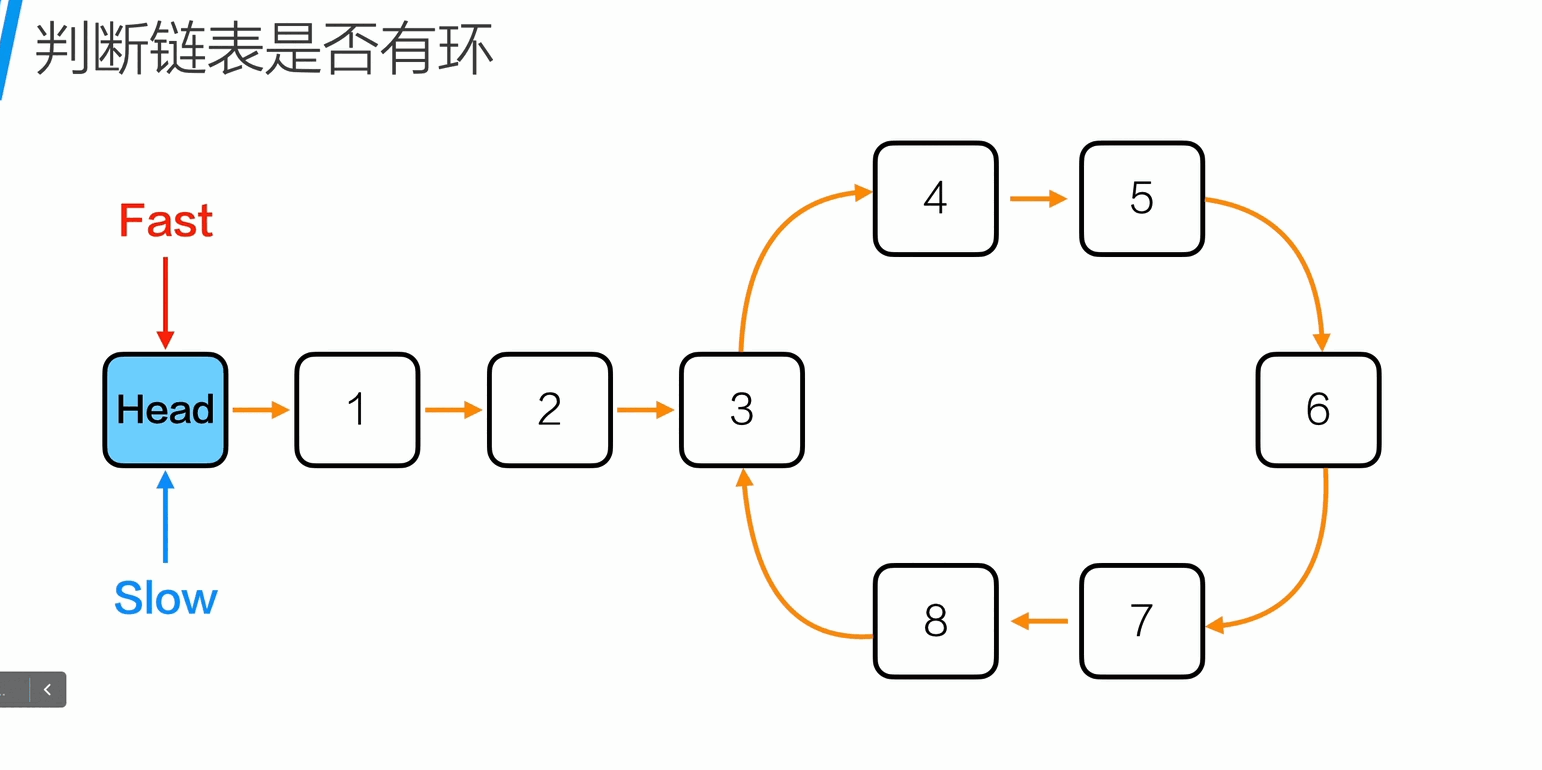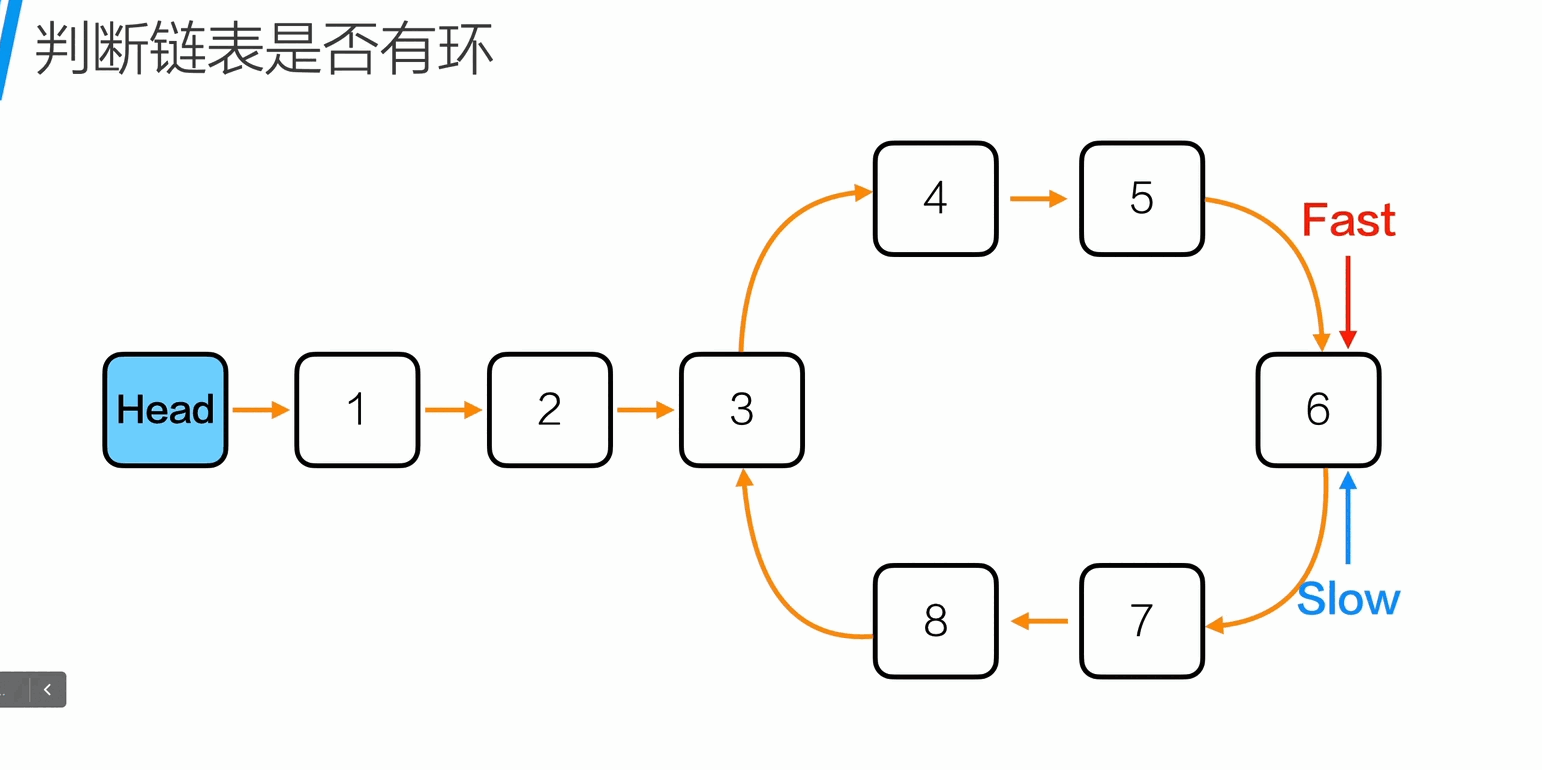
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
int isCycle(Node *head){
Node *fast = head;
Node *slow = head;
while(fast != NULL && fast->next != NULL){
fast = fast->next->next;
slow = slow->next;
if(fast == slow){
return 1;
}
}
return 0;
}
|
链表有环入口在哪里?

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
Node *findBegin(Node *head){
Node *fast = head;
Node *slow = head;
while(fast != NULL && fast->next != NULL){
fast = fast->next->next;
slow = slow->next;
if(fast == slow){
printf("有环\n");
Node *p = fast;
int count = 1;
while(p->next != slow){
count++;
p = p->next;
}
fast = head;
slow = head;
for (int i = 1; i <= count; ++i){
fast = fast->next;
}
while(fast != slow){
fast = fast->next;
slow = slow->next;
}
return slow;
}
}
return NULL;
}
|
📘 详细解释:
这个函数用来 判断链表是否有环,并 返回环的起始节点(如果有)。
🌀 Step 1:快慢指针判断是否有环
fast 每次走两步,slow 每次走一步。- 如果链表中存在环,
fast 和 slow 终会相遇。 - 如果
fast 到了 NULL,说明无环。
🧮 Step 2:计算环的长度
- 在相遇点处定义一个指针
p = fast。 - 沿着环走一圈,统计经过多少个节点直到再次回到
slow,这就是环的长度 count。
🎯 Step 3:找环的入口
- 让两个指针
fast 和 slow 都从 head 出发。 - 先让
fast 多走 count 步,然后两个指针一起向前。 - 当
fast == slow 时,就是环的起始入口节点。
1
2
3
4
| A -> B -> C -> D -> E
^ |
| v
H <- G <- F
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
| #include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <time.h>
#include <ctype.h>
typedef int ElemType;
typedef struct node{
ElemType data;
struct node * next;
}Node;
Node * InitList(){
Node * link = (Node *)malloc(sizeof(Node));
link->data = 0;
link->next = NULL;
return link;
}
Node * get_tail(Node * L){
Node * p = L;
while(p->next != NULL){
p = p->next;
}
return p;
}
Node * insertTail(Node * tail, ElemType e){
Node * p = (Node *)malloc(sizeof(Node));
p->data = e;
tail->next = p;
p->next = NULL;
return p;
}
void freeList(Node * L){
Node * p = L->next;
Node * q;
while(p !=NULL){
q = p->next;
free(p);
p = q;
}
L->next = NULL;
}
void printlistNode(Node * L){
Node * p = L->next;
while(p != NULL){
printf("%d -> ", p->data);
p = p->next;
}
printf("NULL\n");
}
int isCycle(Node *head){
Node *fast = head;
Node *slow = head;
while(fast != NULL && fast->next != NULL){
fast = fast->next->next;
slow = slow->next;
if(fast == slow){
return 1;
}
}
return 0;
}
Node *findBegin(Node *head){
Node *fast = head;
Node *slow = head;
while(fast != NULL && fast->next != NULL){
fast = fast->next->next;
slow = slow->next;
if(fast == slow){
printf("有环\n");
Node *p = fast;
int count = 1;
while(p->next != slow){
count++;
p = p->next;
}
fast = head;
slow = head;
for (int i = 1; i <= count; ++i){
fast = fast->next;
}
while(fast != slow){
fast = fast->next;
slow = slow->next;
}
printf("环入口为:%d\n", slow->data);
return slow;
}
}
return NULL;
}
void printCycleList(Node *head){
Node *entry = findBegin(head);
if(entry == NULL){
printlistNode(head);
return;
}
Node *p = head->next;
while(p != entry){
printf("%d -> ", p->data);
p = p->next;
}
Node *start = entry;
do{
printf("%d -> ", p->data);
p = p->next;
}while(p != start);
printf("(回到 %d)\n", start->data);
}
int main(int argc, char const *argv[])
{
Node * list = InitList();
Node * tail = get_tail(list);
for (int i = 1; i <= 3; ++i){
tail = insertTail(tail, i);
}
Node *three = tail;
tail = insertTail(tail, 4);
tail = insertTail(tail, 5);
tail = insertTail(tail, 6);
tail = insertTail(tail, 7);
tail = insertTail(tail, 8);
tail->next = three;
printCycleList(list);
return 0;
}
|
三、双向链表
链式存储结构的节点中只有一个指示直接后继的指针域,由此,从某个结点出发只能顺指针向后寻查其他节点。
若要寻查结点的直接前驱、则必须从表头指针出发。
换句话说,在单链表中,查找直接后继的执行时间为 \(O(1)\) ,而查找直接前驱的执行时间为 \(O(n)\) 为克服单链表这种单向性的缺点,可利用双向链表(Double Linked List)。
在双向链表的节点中有两个指针域,一个指向直接后继,另一个指向直接前驱。

初始化
插入数据
头插法
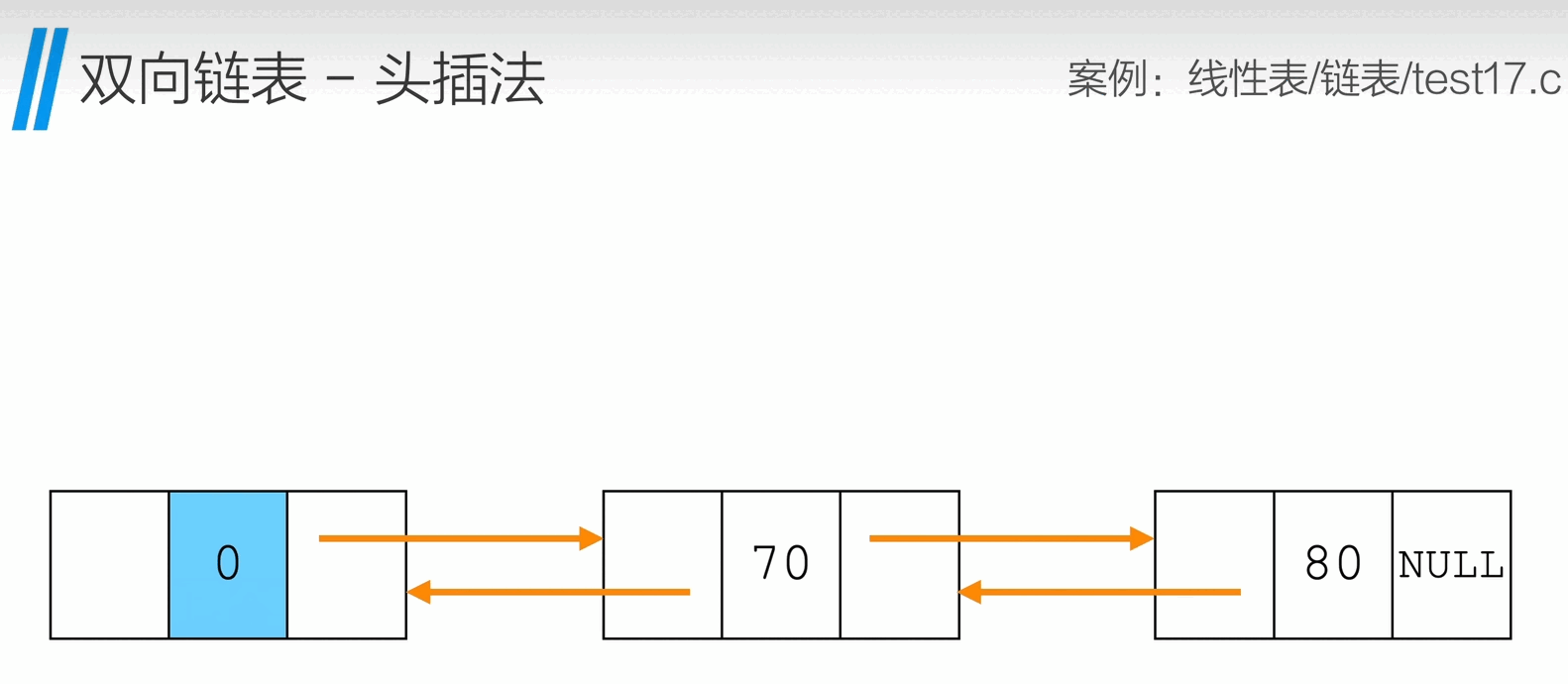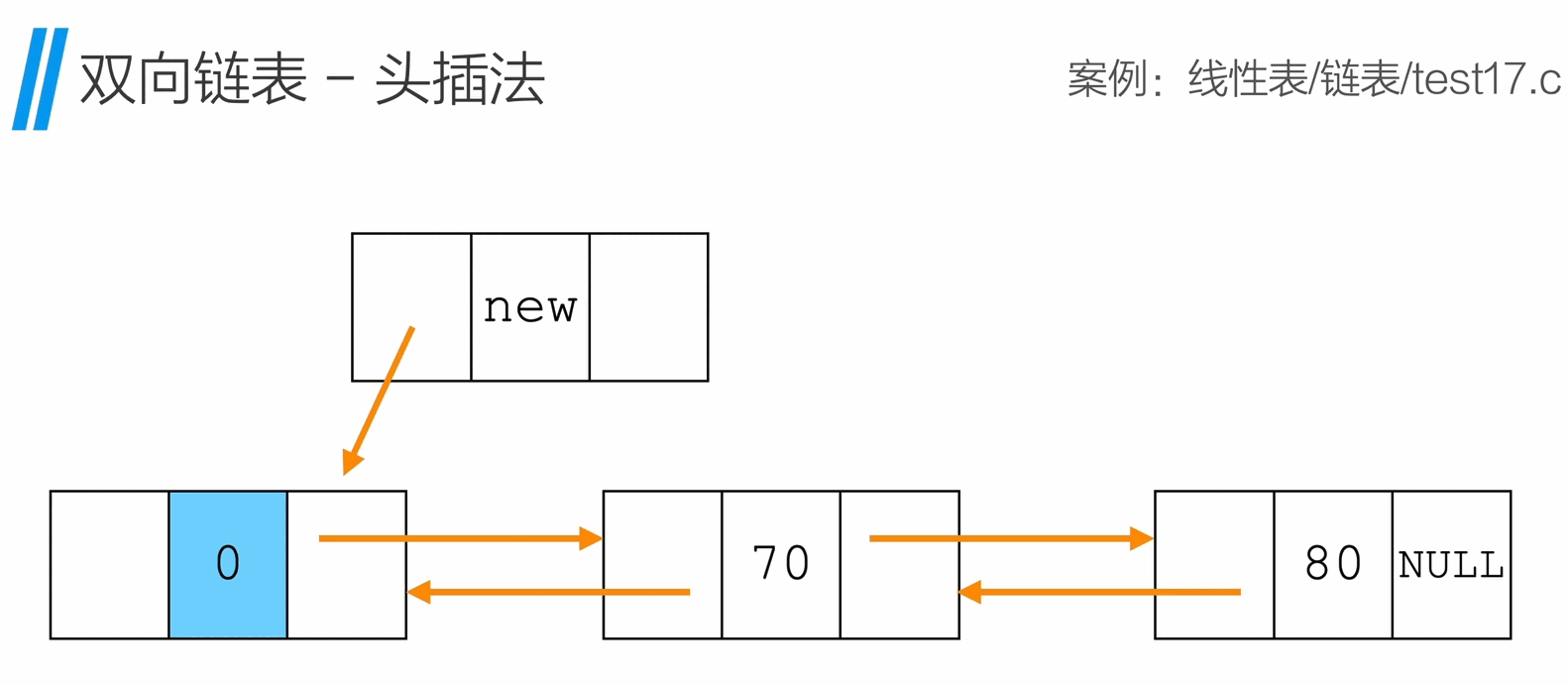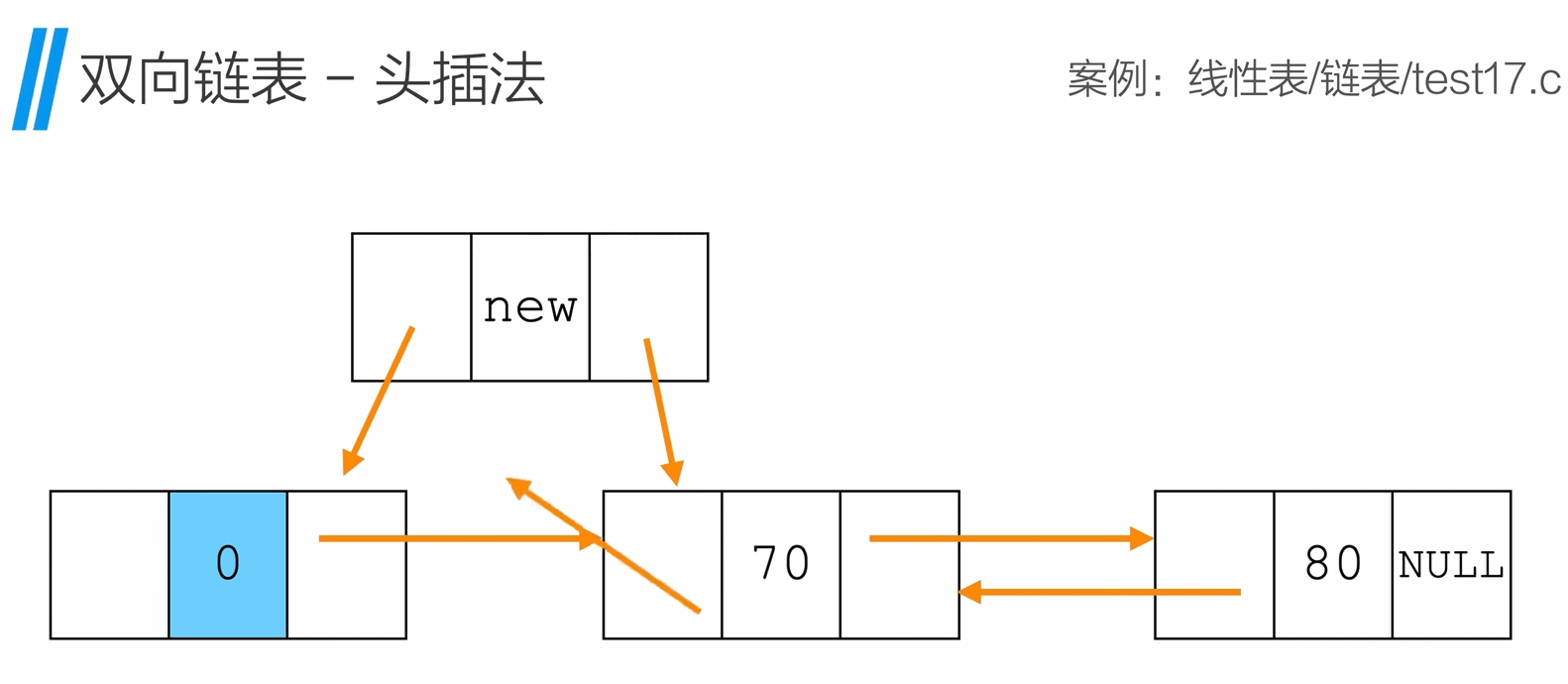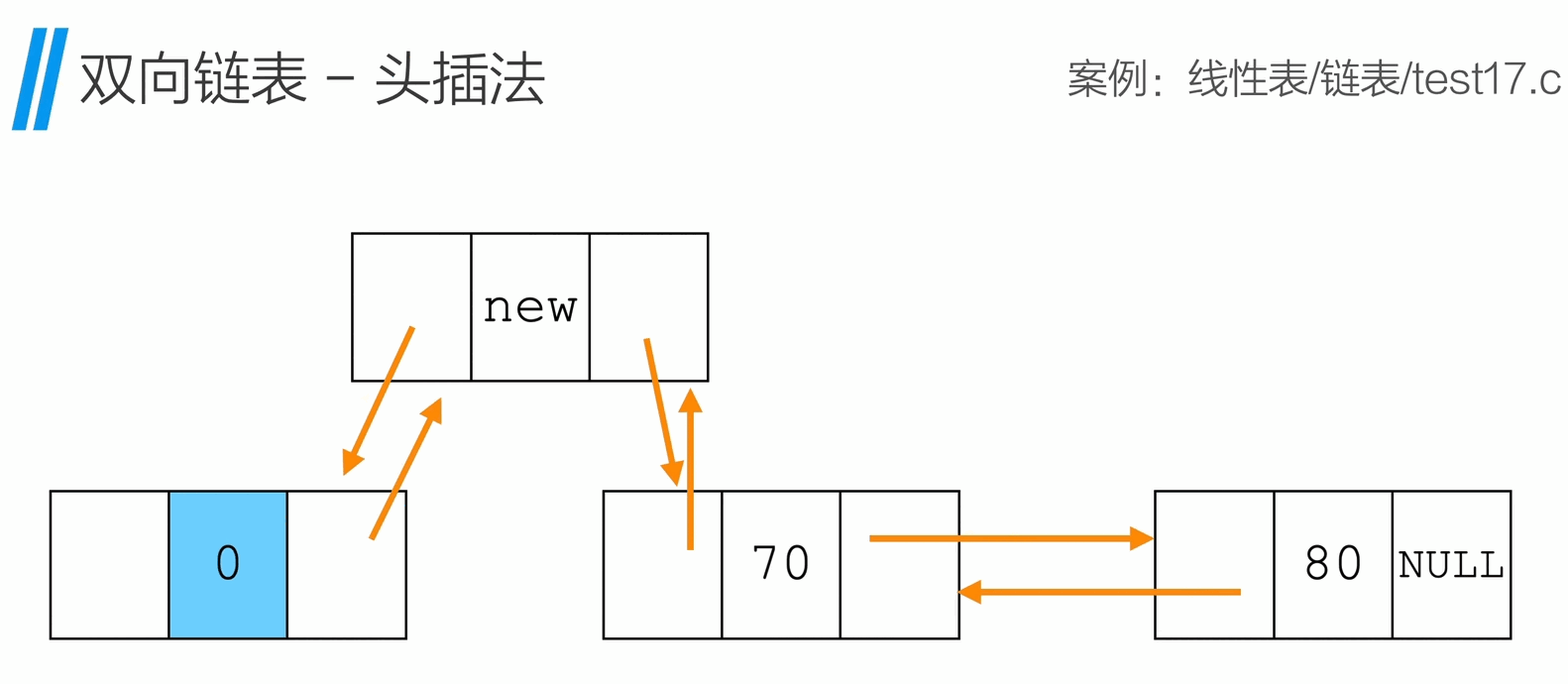
1
2
3
4
5
6
7
8
9
10
11
12
|
int InsertHead(Node * head, ElemType e){
Node * p = (Node *)malloc(sizeof(Node));
p->data = e;
p->next = head->next;
if(head->next != NULL){
head->next->prev = p;
}
head->next = p;
p->prev = head;
return 1;
}
|
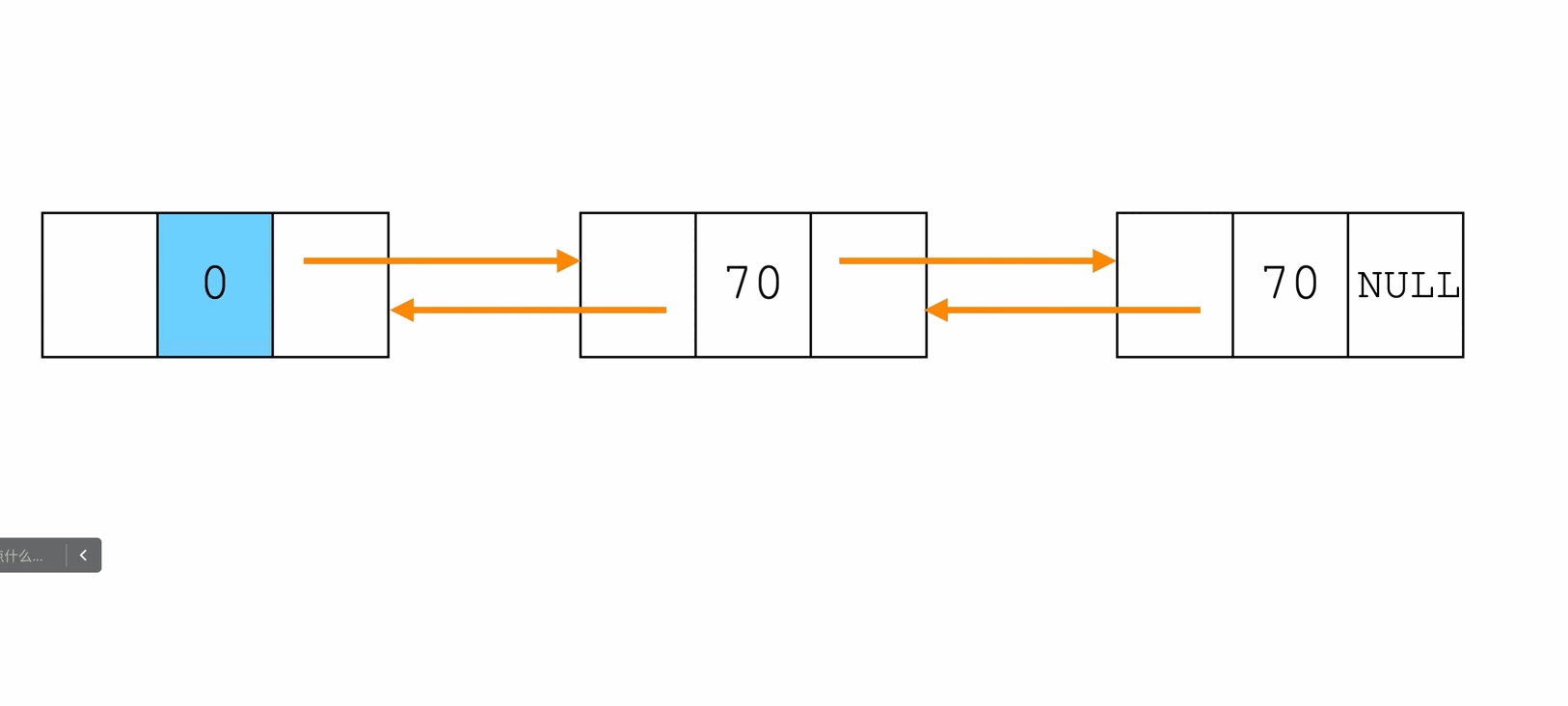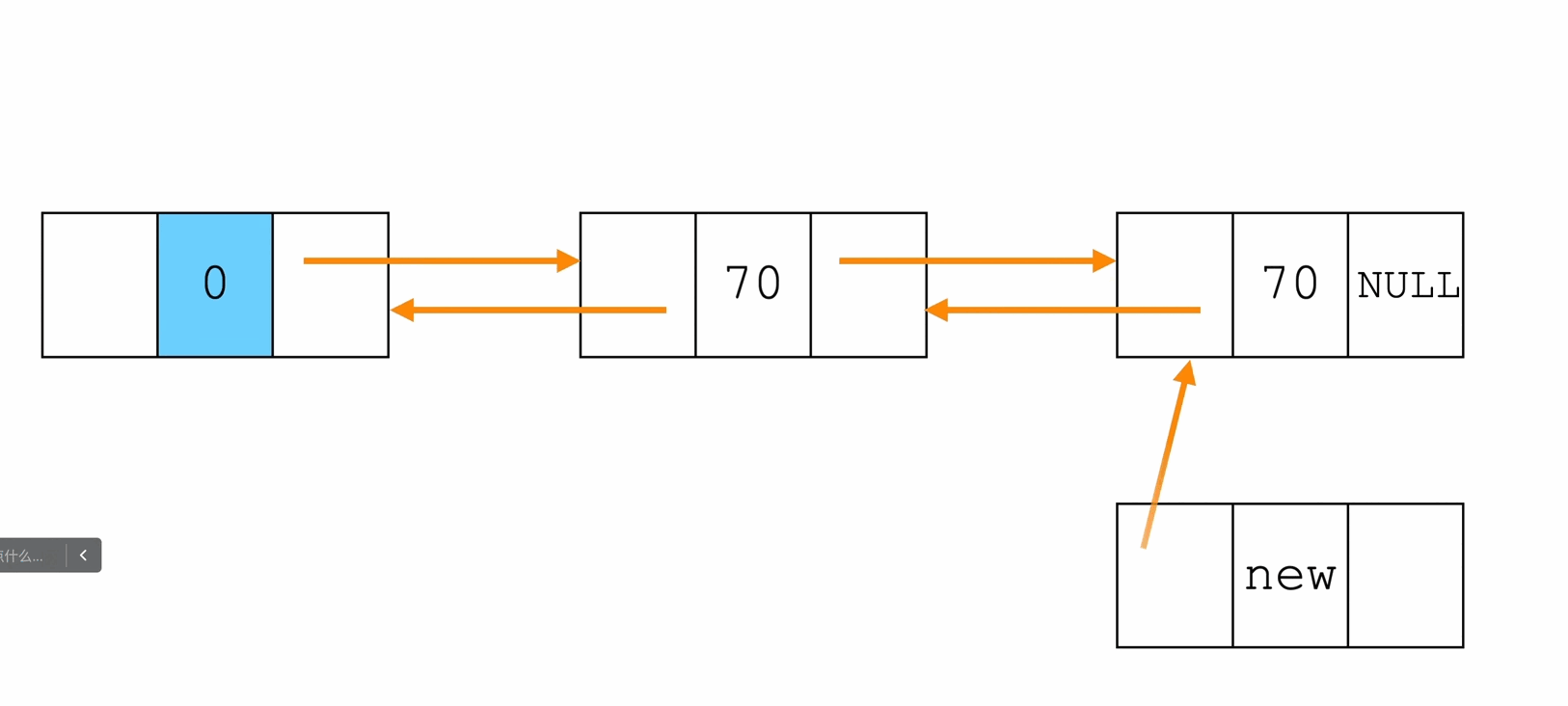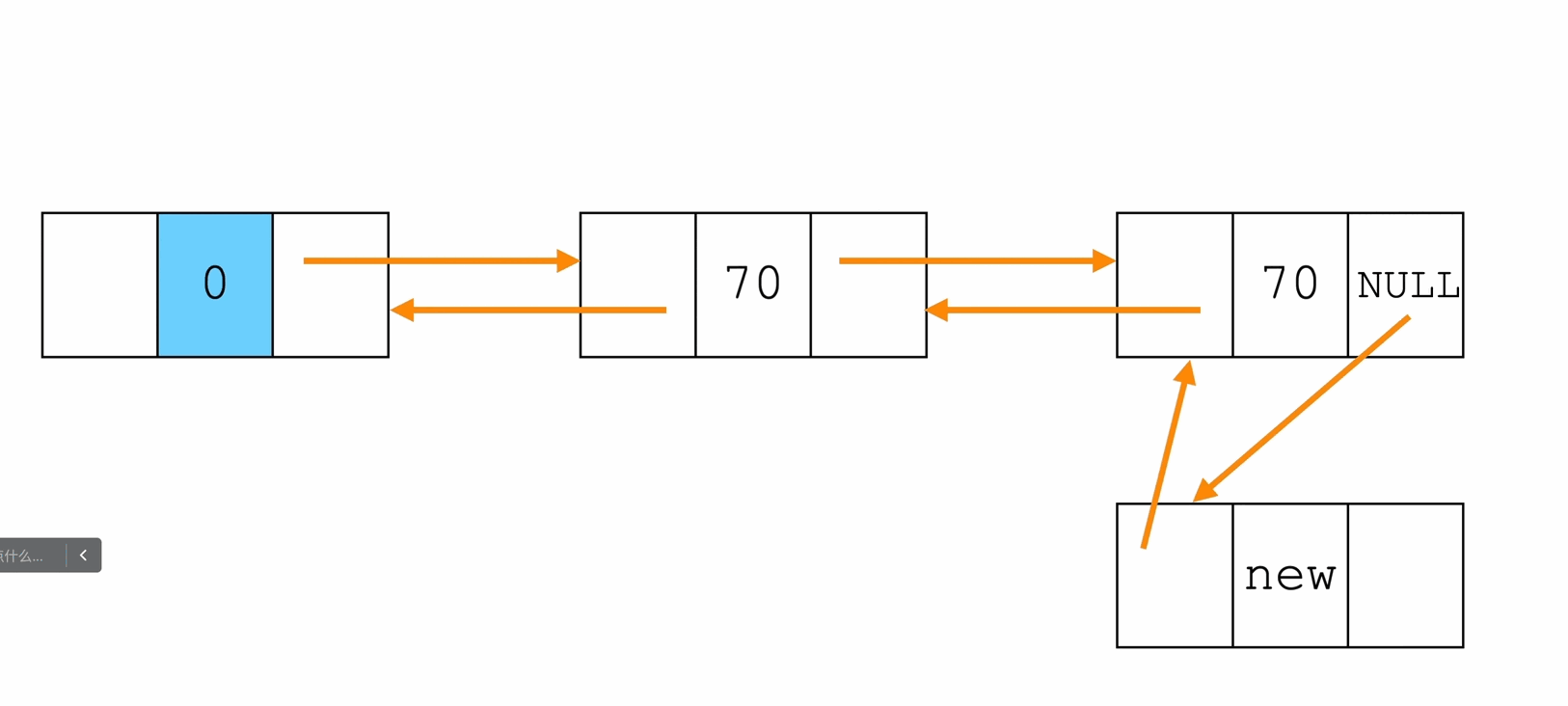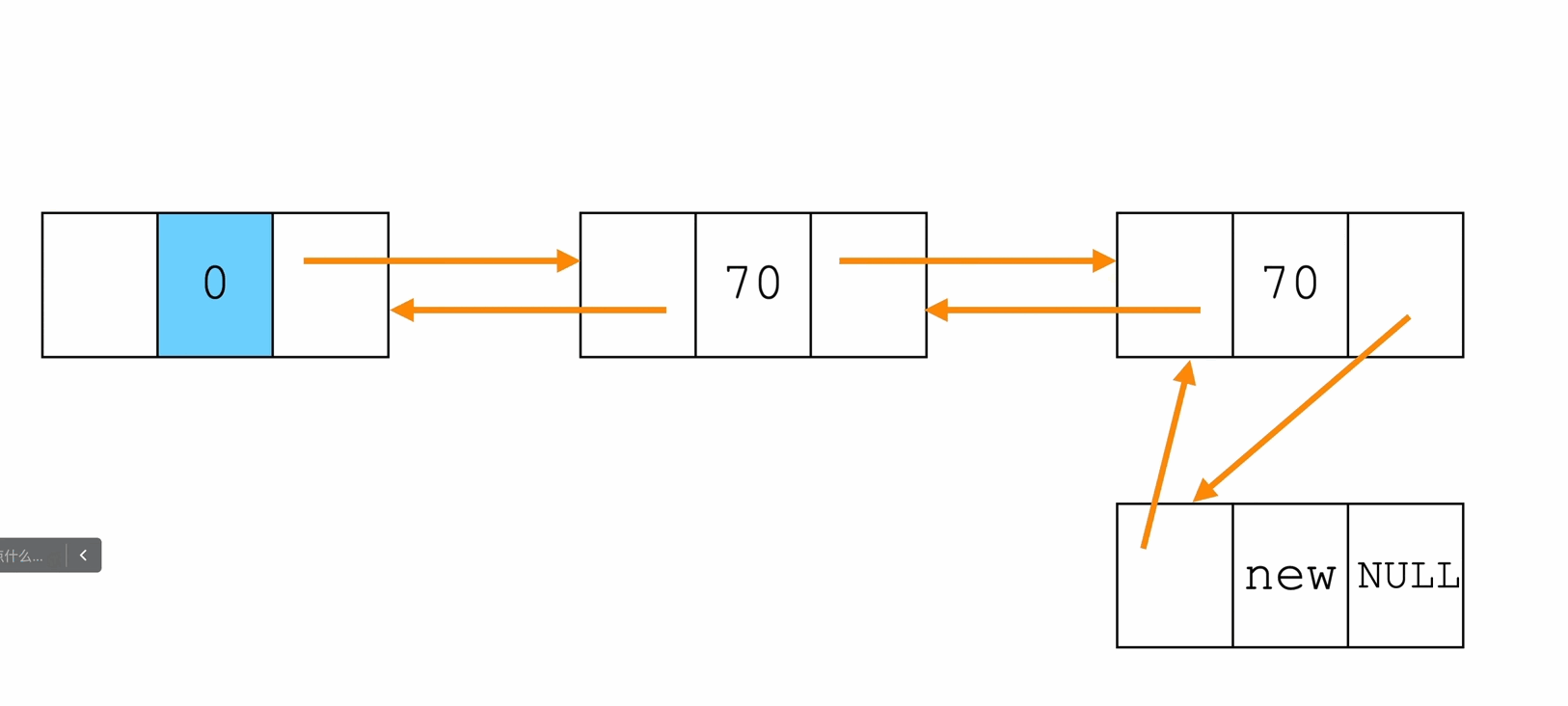
尾插法
1
2
3
4
5
6
7
8
9
10
11
12
13
|
Node * InsertTail(Node * head, ElemType e){
Node * p = (Node *)malloc(sizeof(Node));
p->data = e;
p->next = NULL;
Node * tail = head;
while(tail->next != NULL){
tail = tail->next;
}
tail->next = p;
p->prev = tail;
return p;
}
|
指定位置插入数据
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
int InsertNode(Node * head, int pos, ElemType e){
Node * front = head;
int i = 0;
while(i < pos - 1){
front = front->next;
i++;
if(front == NULL){
return 0;
}
}
Node * p = (Node *)malloc(sizeof(Node));
p->data = e;
p->next = front->next;
if(front->next != NULL){
front->next->prev = p;
}
front->next = p;
p->prev = front;
return 1;
}
|
删除节点
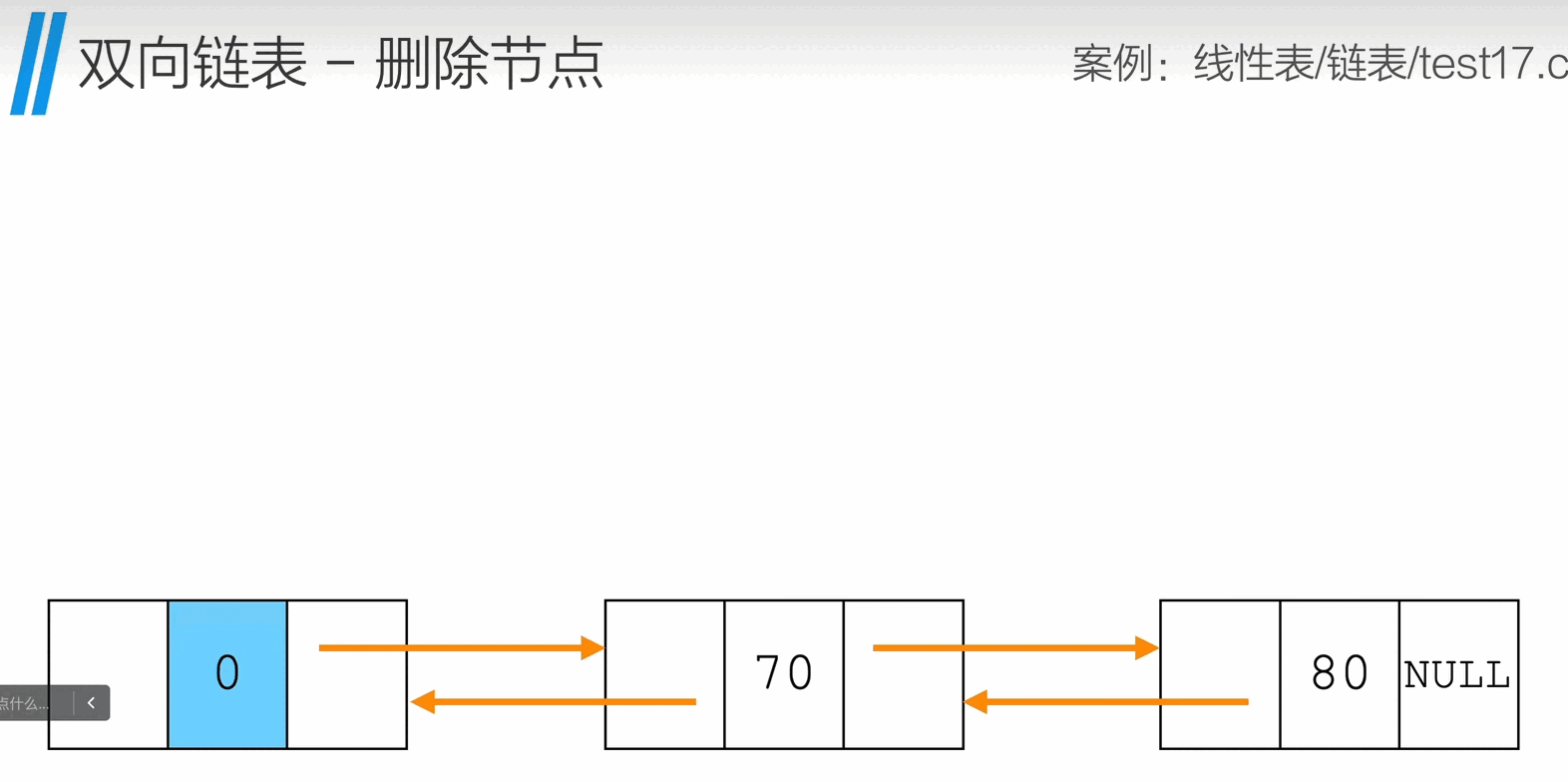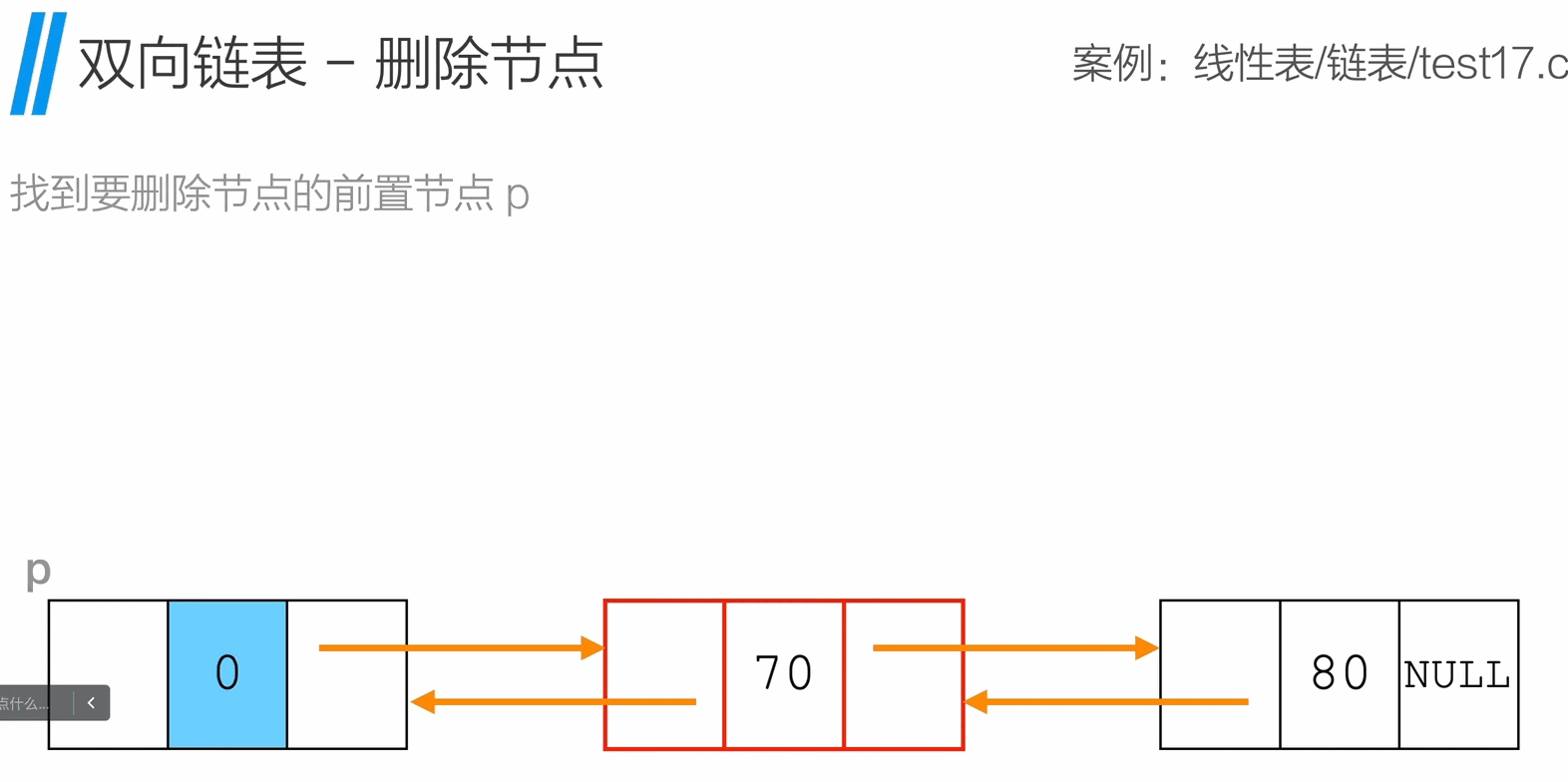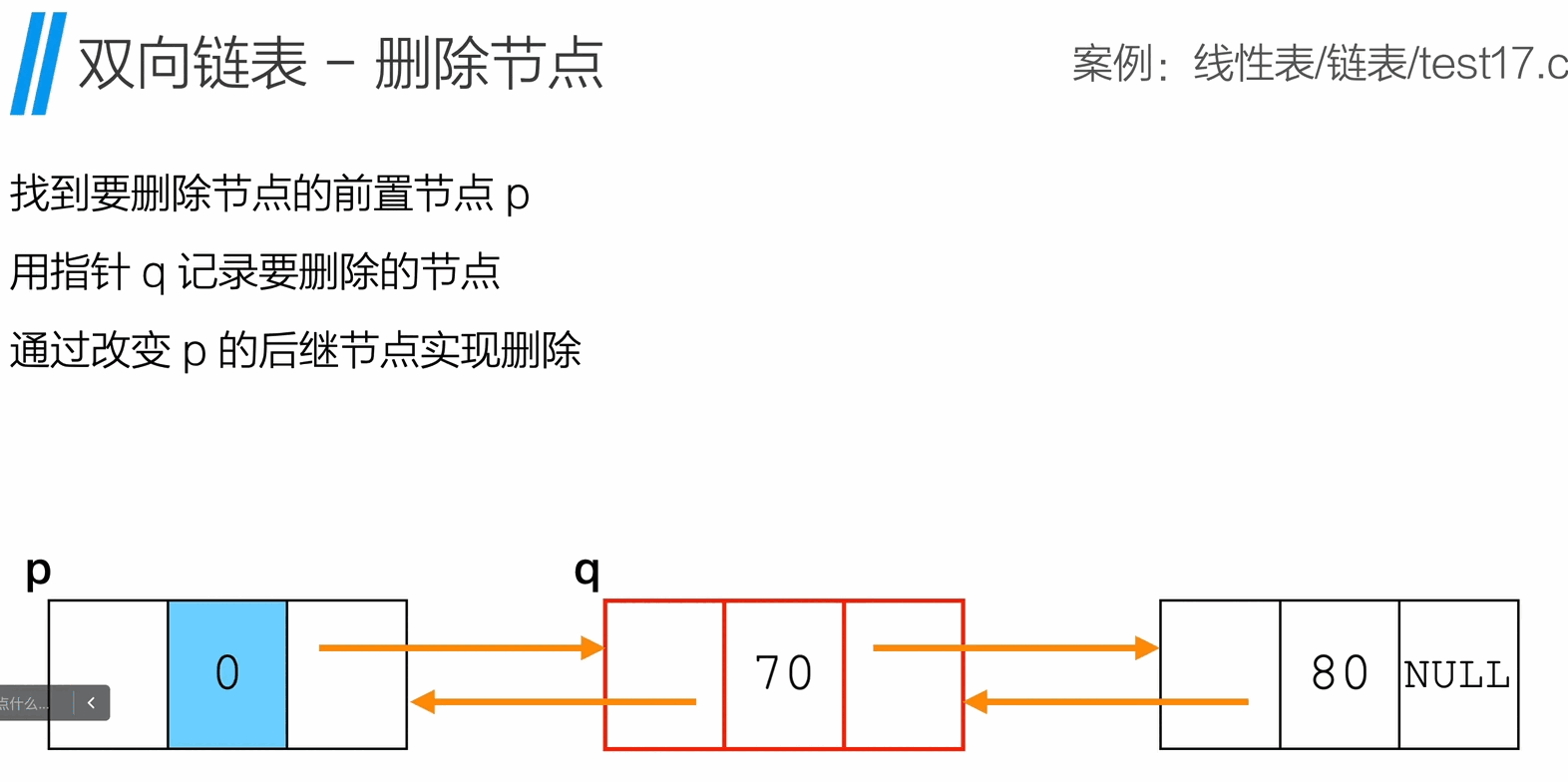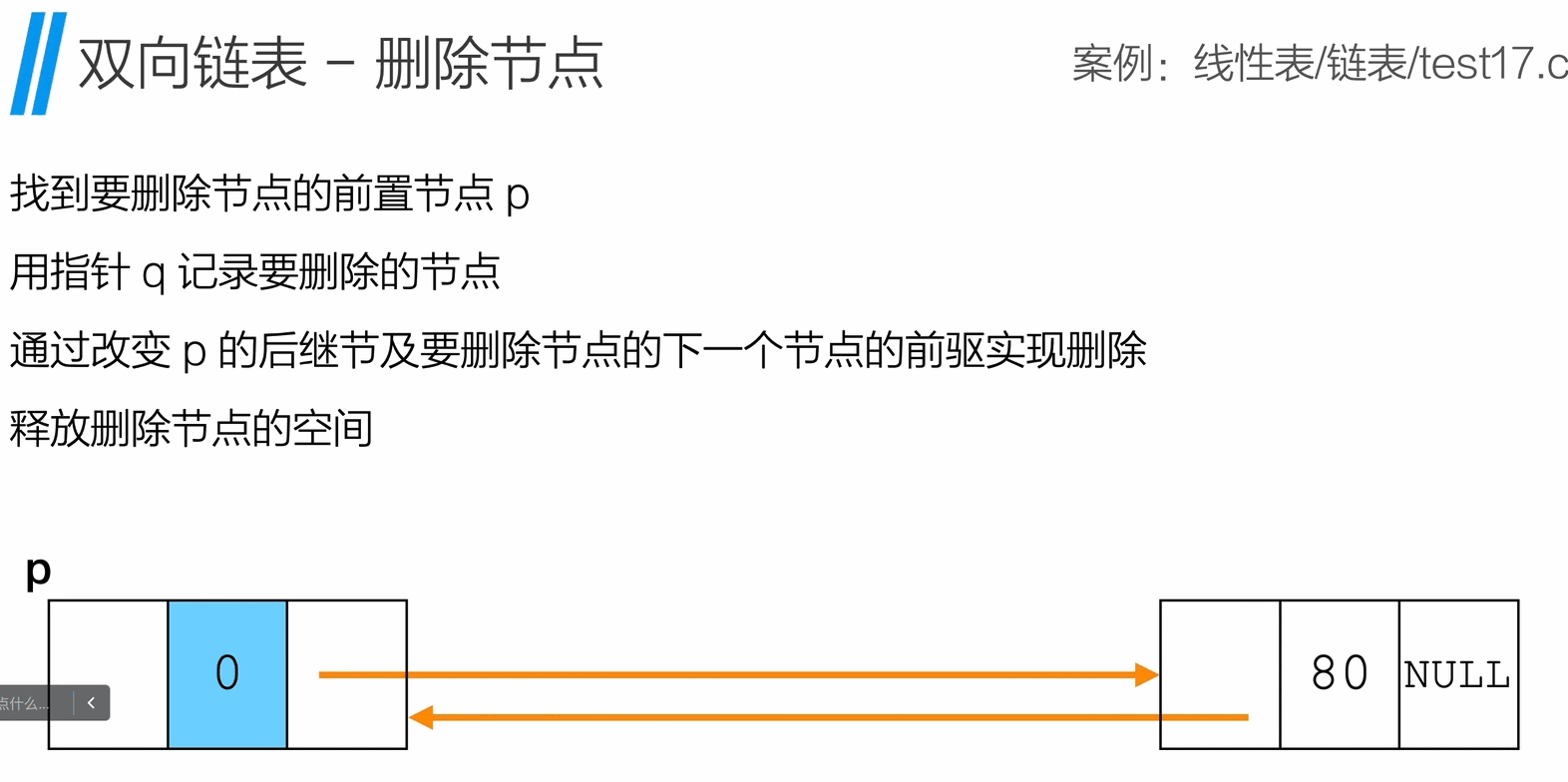
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
int DeleteNode(Node * head, int pos){
Node * front = head;
int i = 0;
while(i < pos - 1){
front = front->next;
i++;
if(front == NULL){
return 0;
}
}
if(front->next == NULL){
printf("没有节点可以删除\n");
return 0;
}
Node * p = front->next;
front->next = p->next;
if(p->next != NULL){
p->next->prev = front;
}
free(p);
return 1;
}
|
顺序表 VS 链表
| 比较项目 | 顺序表 | 链表 |
|---|
| 空间 | | |
| 存储空间 | 预先分配,会出现闲置或溢出现象 | 动态分配,不会出现存储空间闲置或溢现象 |
| 存储密度 | 不用为表示节点间的逻辑关系而增加额外的存储,存储密度等于 1 | 需要借助指针来体现元素间的逻辑关系,存储密度小于 1 |
| 时间 | | |
| 存取元素 | 随机存取,按位置访问元素的时间复杂度为 O(1) | 顺序存取,按位置访问元素时间复杂度为 O(n) |
| 插入、删除 | 平均移动约表中一半元素,时间复杂度为 O(n) | 不需要移动元素,确定插入、删除位置后,时间复杂度为 O(1) |
| 适用情况 | | |
| 1. 表长变化不大,且能事先确定变化的范围2. 很少进行插入或删除操作,经常按元素位置序号访问数据元素 | 1. 长度变化较大2. 频繁进行插入或删除操作 |
顺序表:不频繁插入删除,能事先确定这个大小长度,经常按位置访问元素
链表:长度变化大,频繁进行插入删除操作
N、应用
查找倒数k个节点

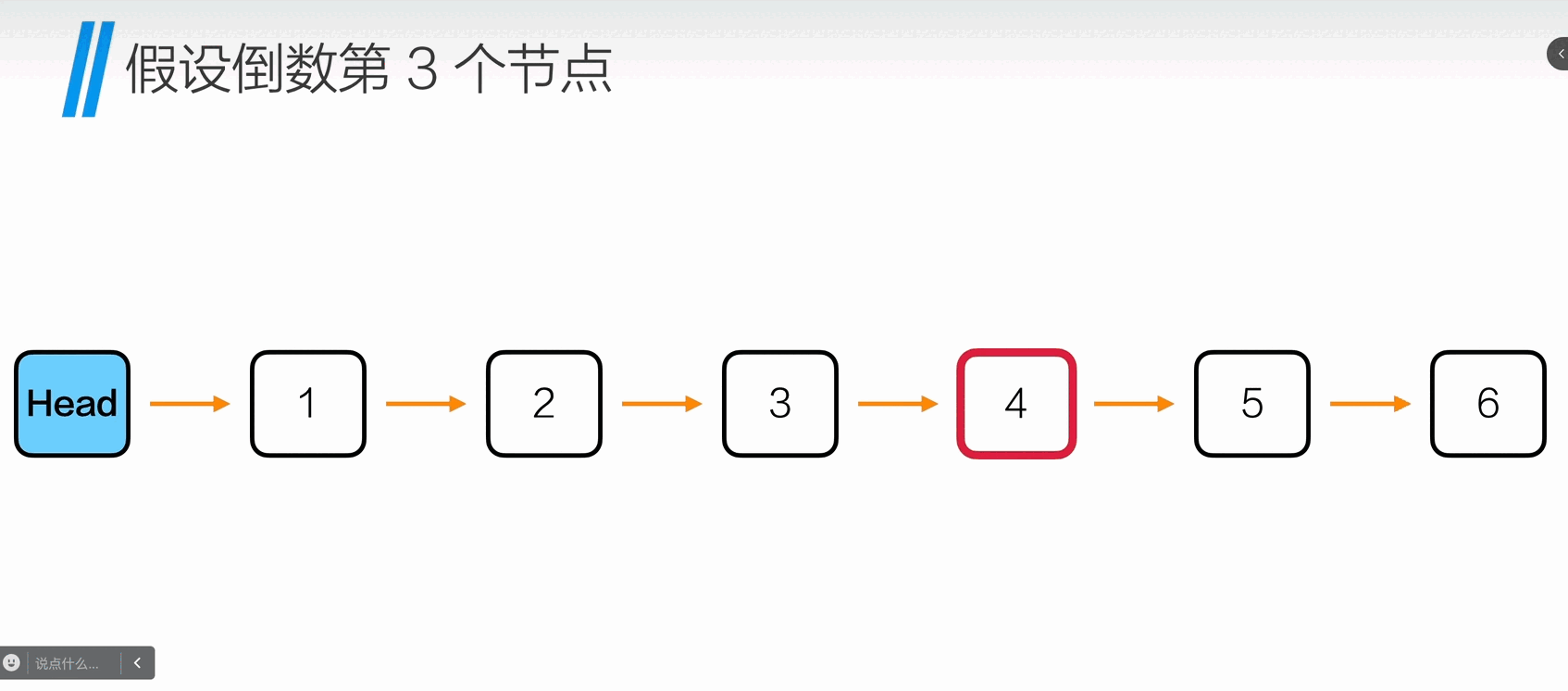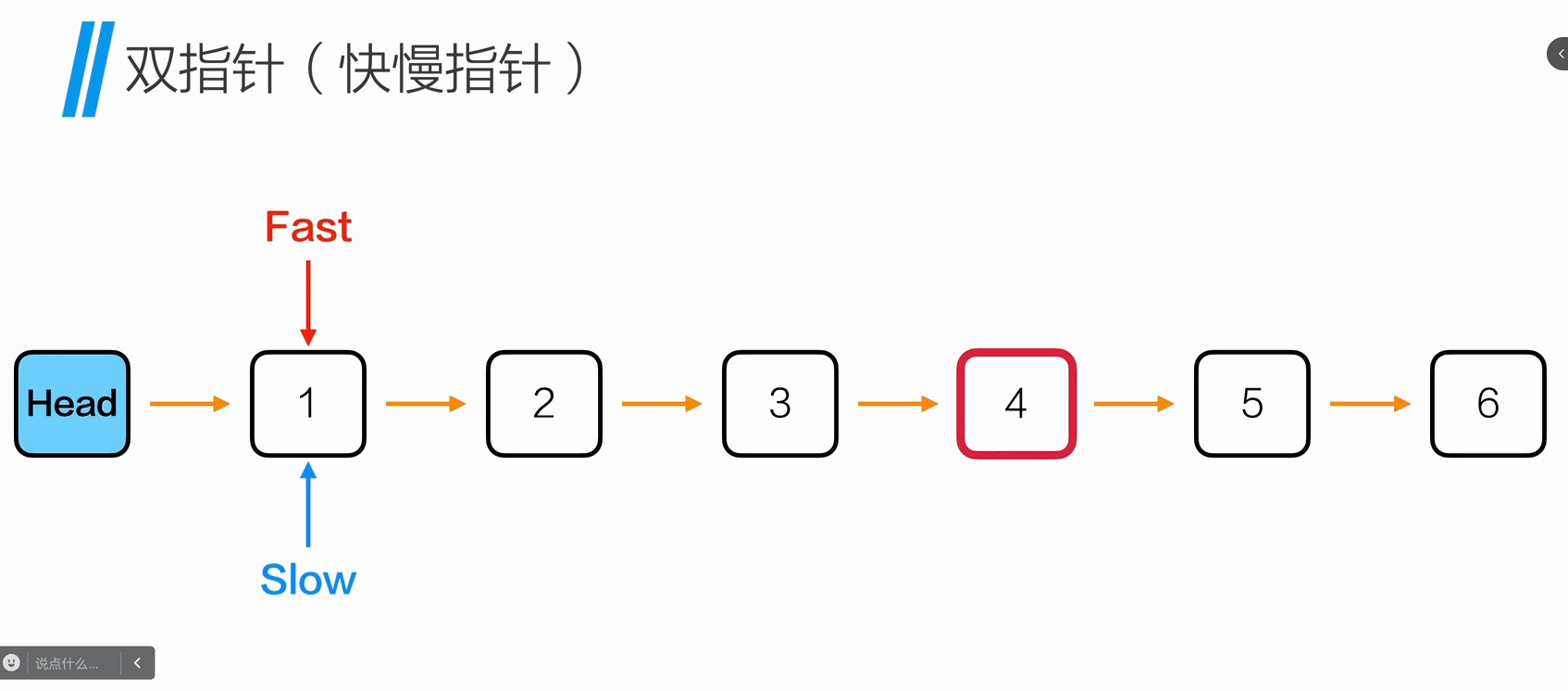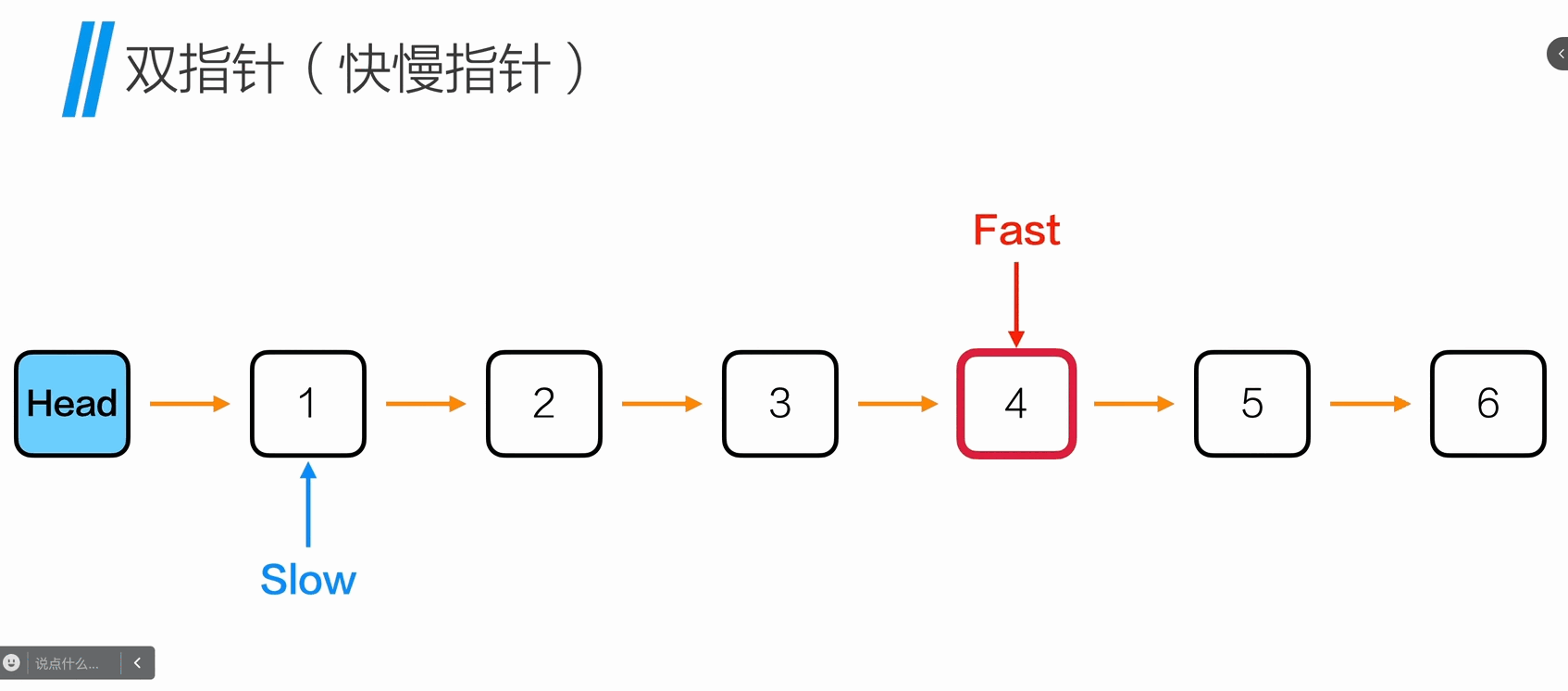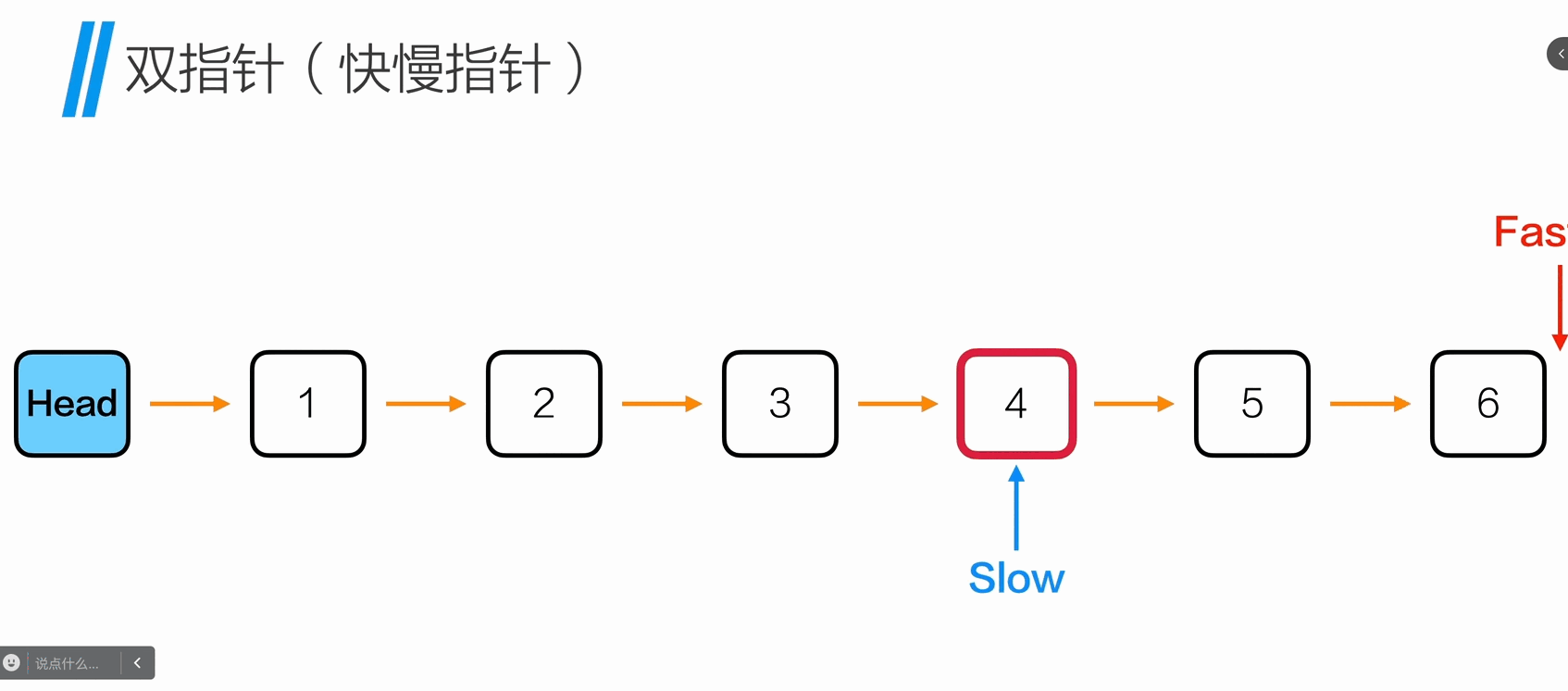
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
int findNodeFS(Node * L, int k){
Node * fast = L->next;
Node * slow = L->next;
int i = 0;
while(i < k){
if (fast == NULL) {
printf("链表长度小于 %d,无法找到该节点。\n", k);
return -1;
}
fast = fast->next;
i++;
}
while(fast != NULL){
fast = fast->next;
slow = slow->next;
}
printf("倒数第 %d 个位置的结点为:%d \n",k, slow->data );
return 1;
}
|
找两个链表想同的地址
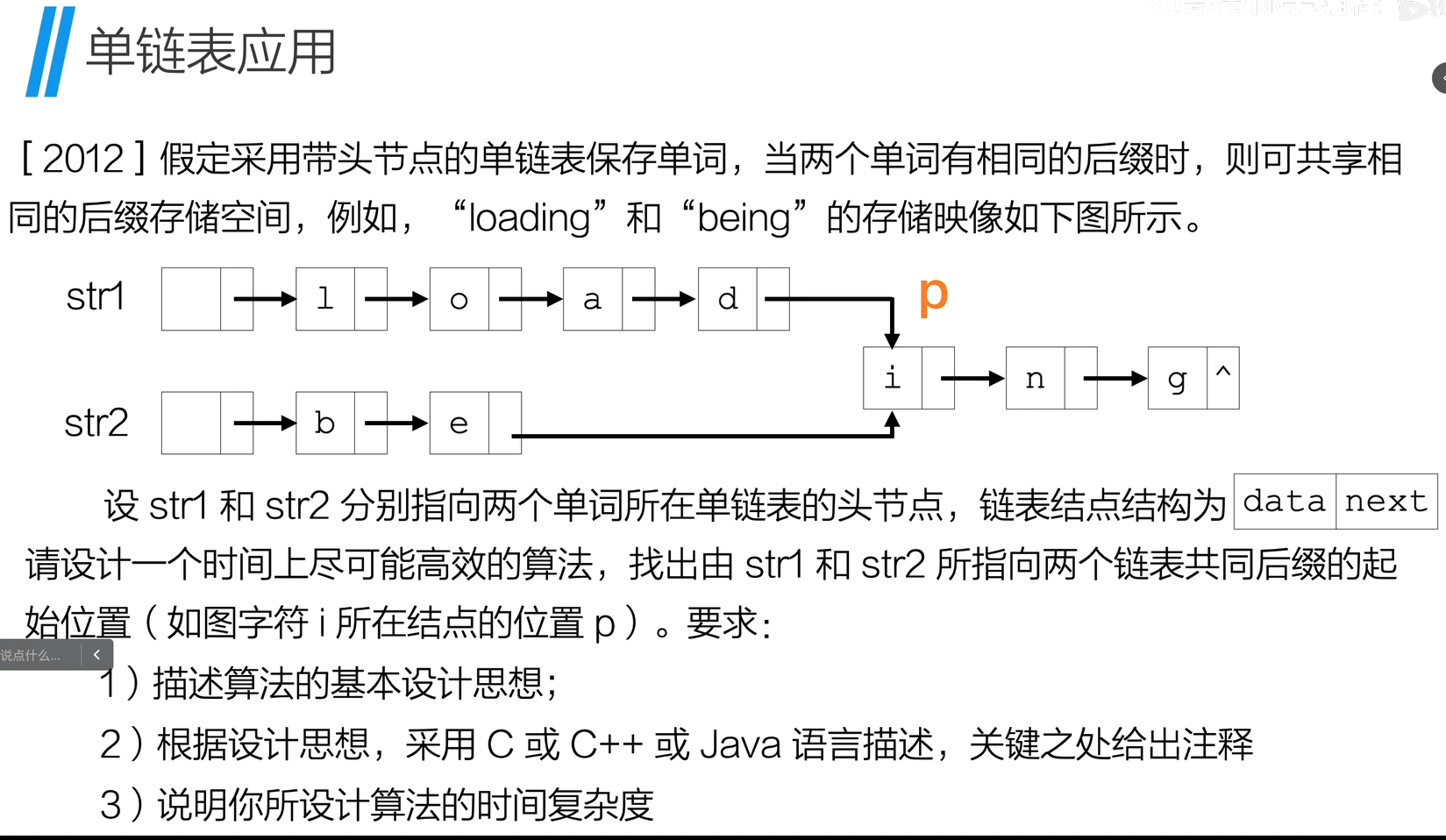
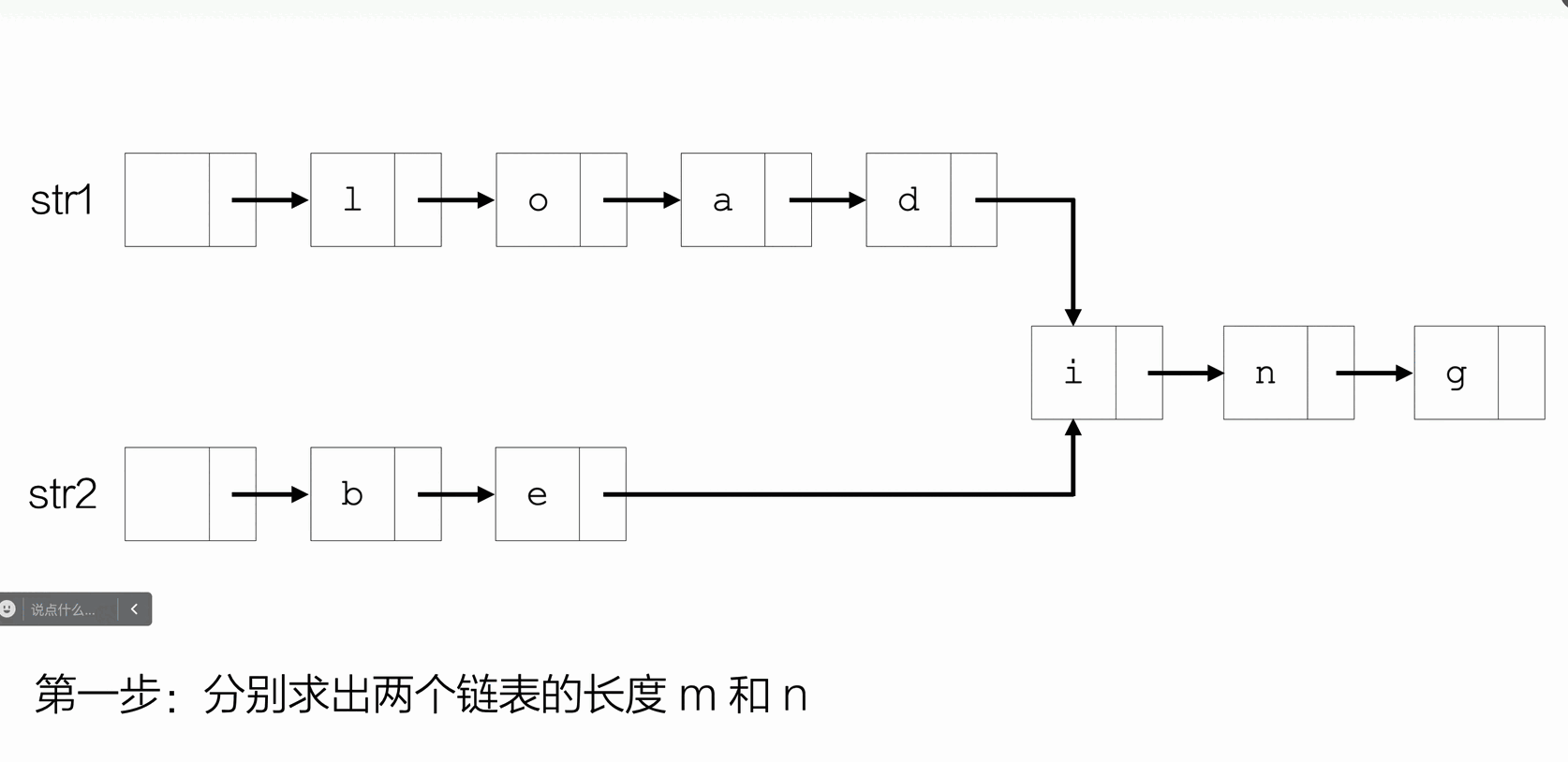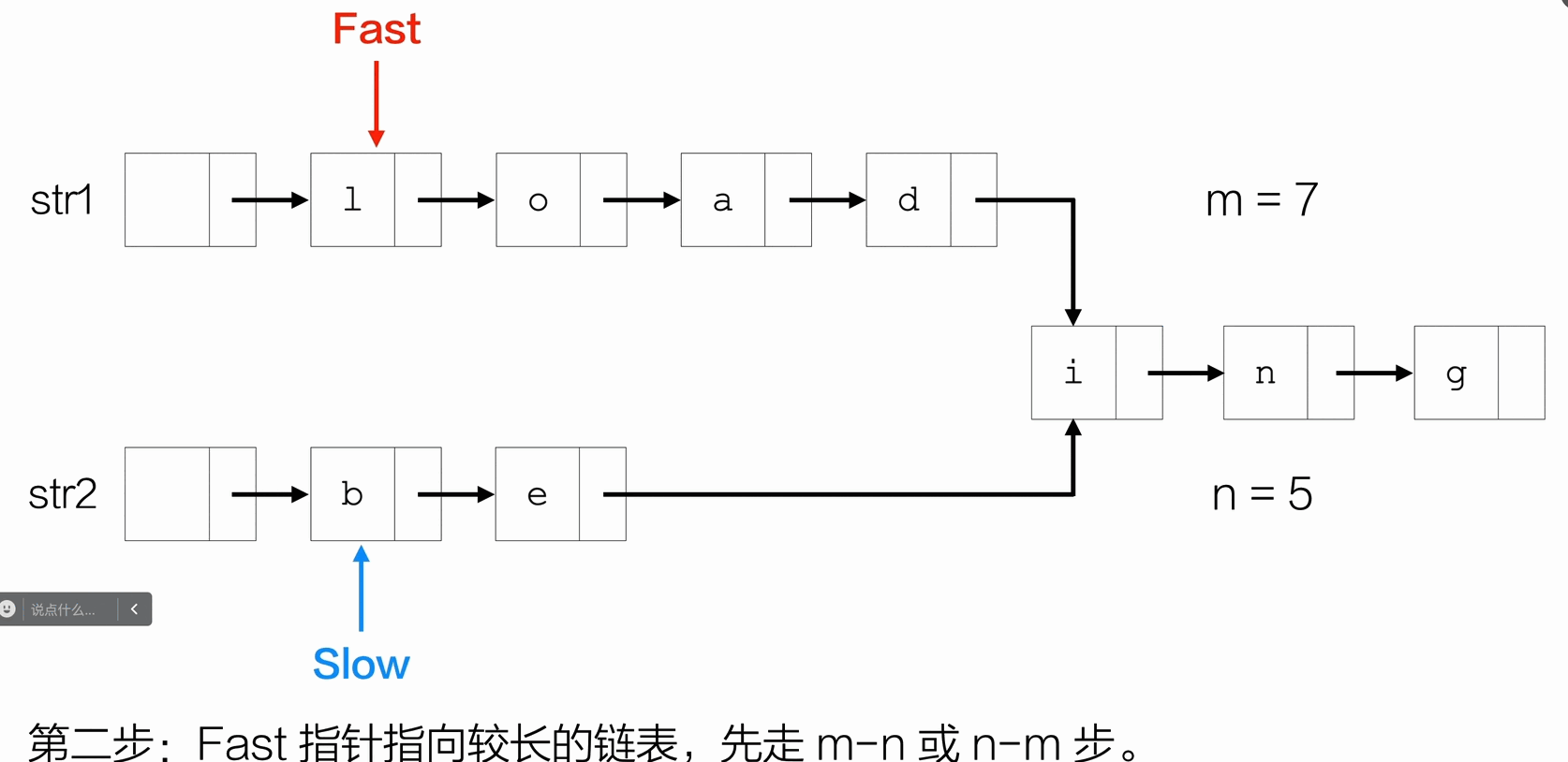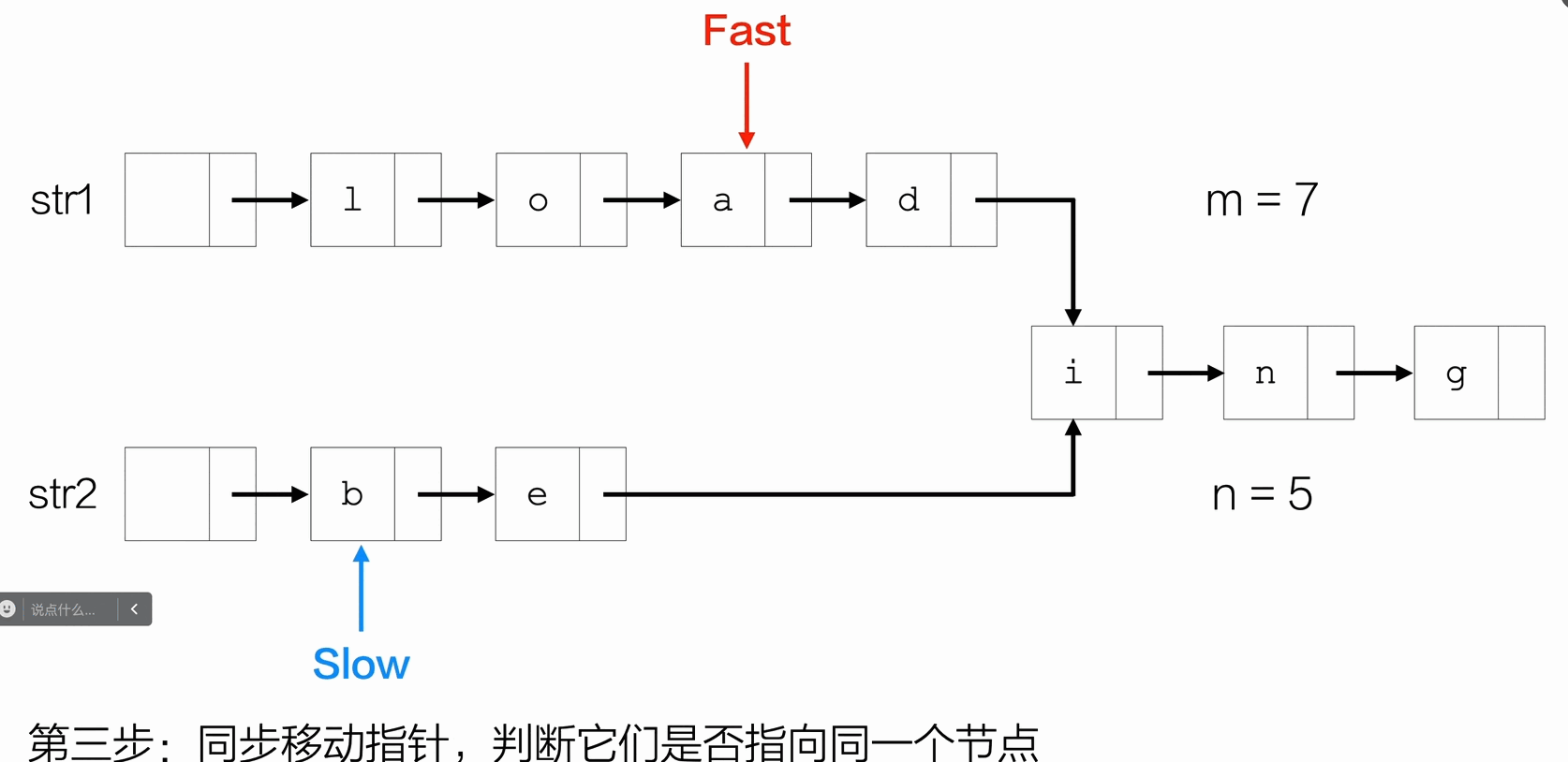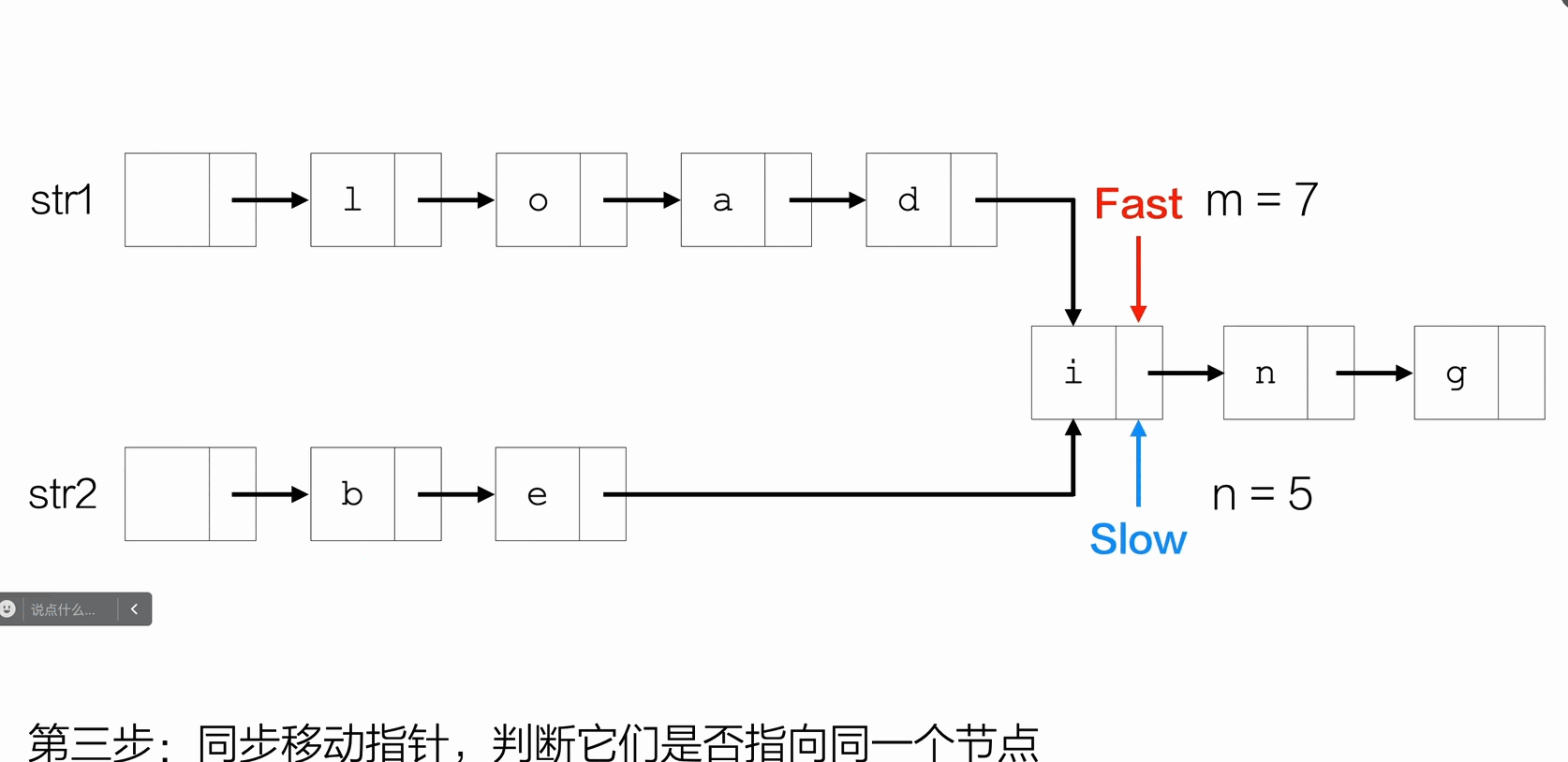
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
| #include <stdio.h>
#include <stdlib.h>
typedef char ElemType;
typedef struct node {
ElemType data;
struct node *next;
} Node;
Node *InitList() {
Node *link = (Node *)malloc(sizeof(Node));
link->data = 0;
link->next = NULL;
return link;
}
Node *insertTail(Node *tail, ElemType e) {
Node *p = (Node *)malloc(sizeof(Node));
p->data = e;
p->next = NULL;
tail->next = p;
return p;
}
int listLength(Node * L){
Node * p = L;
int len = 0;
while(p != NULL){
p = p->next;
len++;
}
return len;
}
void printList(Node *L) {
Node *p = L->next;
while (p != NULL) {
printf("%c -> ", p->data);
p = p->next;
}
printf("NULL\n");
}
Node *buildSharedSuffix() {
Node *i = (Node *)malloc(sizeof(Node));
Node *n = (Node *)malloc(sizeof(Node));
Node *g = (Node *)malloc(sizeof(Node));
i->data = 'i'; i->next = n;
n->data = 'n'; n->next = g;
g->data = 'g'; g->next = NULL;
return i;
}
Node *findCommonNode(Node *str1, Node *str2){
if(str1 == NULL || str2 == NULL){
return NULL;
}
int len1 = listLength(str1);
int len2 = listLength(str2);
Node *fast = (len1 > len2) ? str1->next : str2->next;
Node *slow = (len1 > len2) ? str2->next : str1->next;
int step = (len1 > len2) ? (len1 - len2) : (len2 - len1);
for (int i = 0; i < step; ++i){
fast = fast->next;
}
while(fast != slow){
fast = fast->next;
slow = slow->next;
}
if (fast != NULL) {
printf("共同的后缀起始位置为:%c\n", fast->data);
} else {
printf("两个链表没有共同后缀\n");
}
return fast;
}
void freeList(Node *L, Node *shared) {
Node *p = L->next;
while (p != NULL && p != shared) {
Node *q = p->next;
free(p);
p = q;
}
free(L);
}
int main() {
Node *str1 = InitList();
Node *str2 = InitList();
Node *tail1 = str1;
tail1 = insertTail(tail1, 'l');
tail1 = insertTail(tail1, 'o');
tail1 = insertTail(tail1, 'a');
tail1 = insertTail(tail1, 'd');
Node *tail2 = str2;
tail2 = insertTail(tail2, 'b');
tail2 = insertTail(tail2, 'e');
Node *shared = buildSharedSuffix();
tail1->next = shared;
tail2->next = shared;
printf("str1: ");
printList(str1);
printf("str2: ");
printList(str2);
findCommonNode(str1,str2);
freeList(str1, shared);
freeList(str2, shared);
Node *p = shared;
while (p != NULL) {
Node *q = p->next;
free(p);
p = q;
}
return 0;
}
|
去除绝对值相同的元素

$ n$ 最小值为 \(|data|\) ,本题为 \(21\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
| #include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <time.h>
#include <ctype.h>
typedef int ElemType;
typedef struct node{
ElemType data;
struct node * next;
}Node;
Node * InitList(){
Node * link = (Node *)malloc(sizeof(Node));
link->data = 0;
link->next = NULL;
return link;
}
int insertHead(Node * L, ElemType e){
Node * p = (Node *)malloc(sizeof(Node));
p->data = e;
p->next = L->next;
L->next = p;
return 1;
}
Node * get_tail(Node * L){
Node * p = L;
while(p->next != NULL){
p = p->next;
}
return p;
}
Node * insertTail(Node * tail, ElemType e){
Node * p = (Node *)malloc(sizeof(Node));
p->data = e;
tail->next = p;
p->next = NULL;
return p;
}
void removeNode(Node * L, int n){
Node *p = L;
int index;
int *q = (int *)malloc(sizeof(int) * (n+1));
for (int i = 0; i <= n; ++i){
*(q + i) = 0;
}
while(p->next != NULL){
index = abs(p->next->data);
if(*(q + index) == 0){
*(q + index) = 1;
p = p->next;
}else{
Node *temp = p->next;
p->next = temp->next;
free(temp);
}
}
free(q);
}
void freeList(Node * L){
Node * p = L->next;
Node * q;
while(p !=NULL){
q = p->next;
free(p);
p = q;
}
L->next = NULL;
}
void printlistNode(Node * L){
Node * p = L->next;
while(p != NULL){
printf("%d -> ", p->data);
p = p->next;
}
printf("NULL\n");
}
int main(int argc, char const *argv[])
{
Node * list = InitList();
Node * tail = get_tail(list);
tail = insertTail(tail,21);
tail = insertTail(tail,-15);
tail = insertTail(tail,-15);
tail = insertTail(tail,-7);
tail = insertTail(tail,15);
printlistNode(list);
removeNode(list,21);
printlistNode(list);
freeList(list);
printlistNode(list);
return 0;
}
|
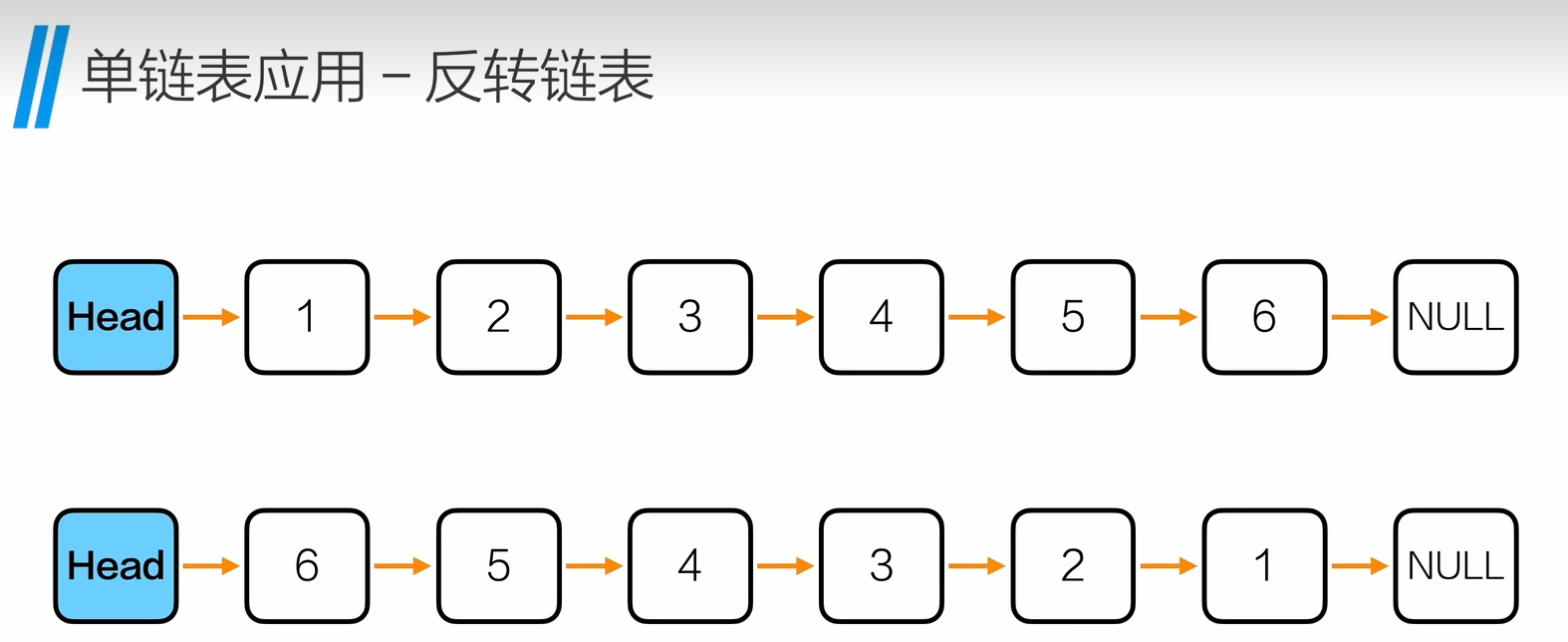
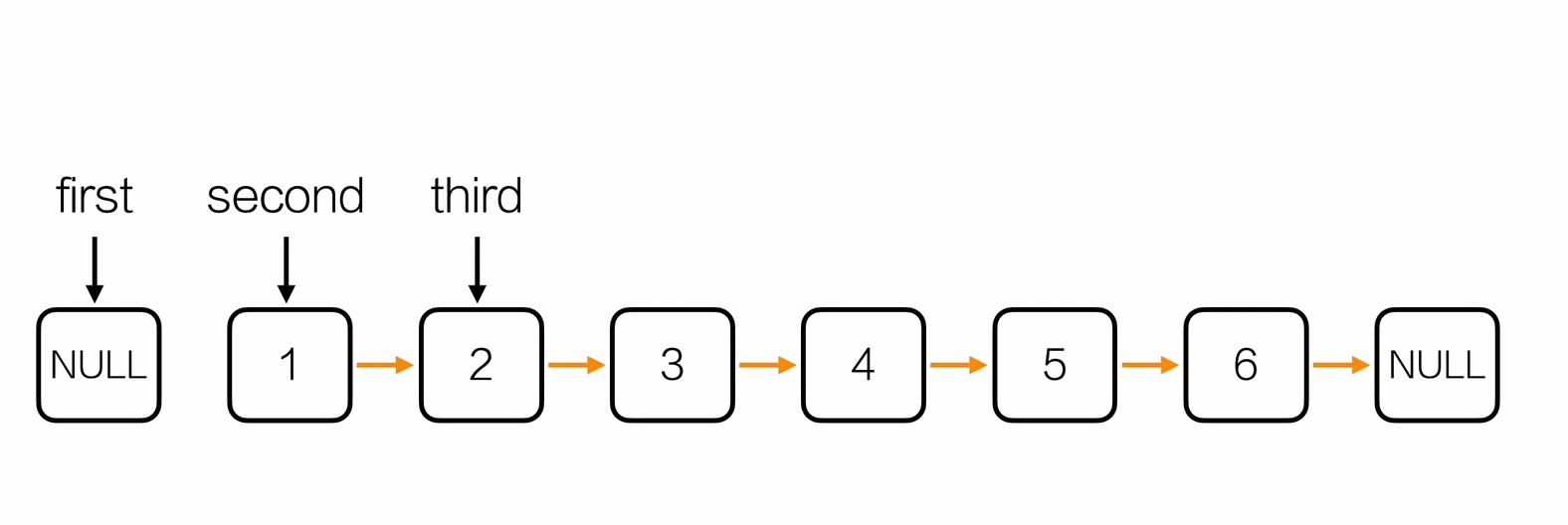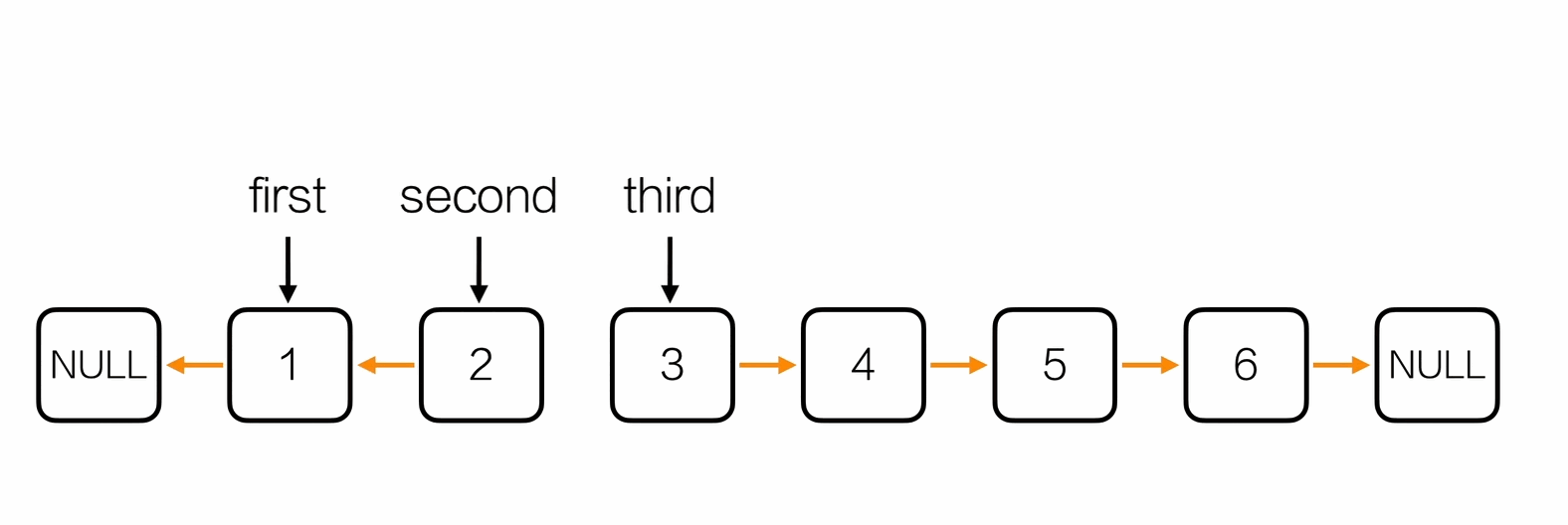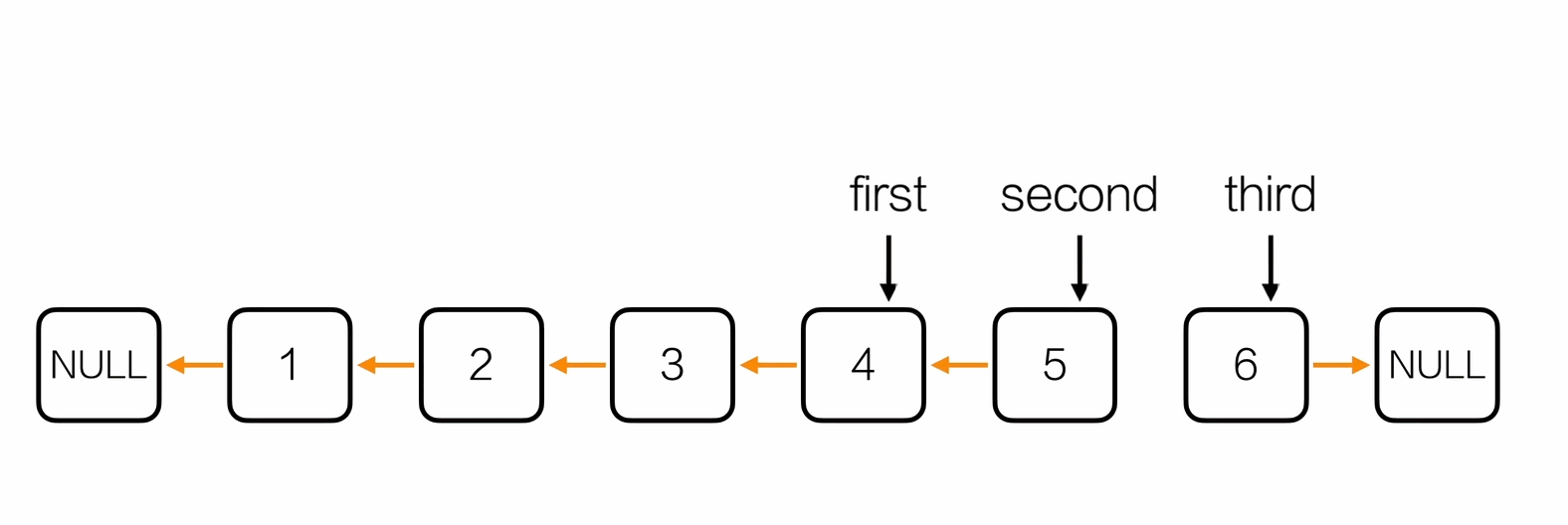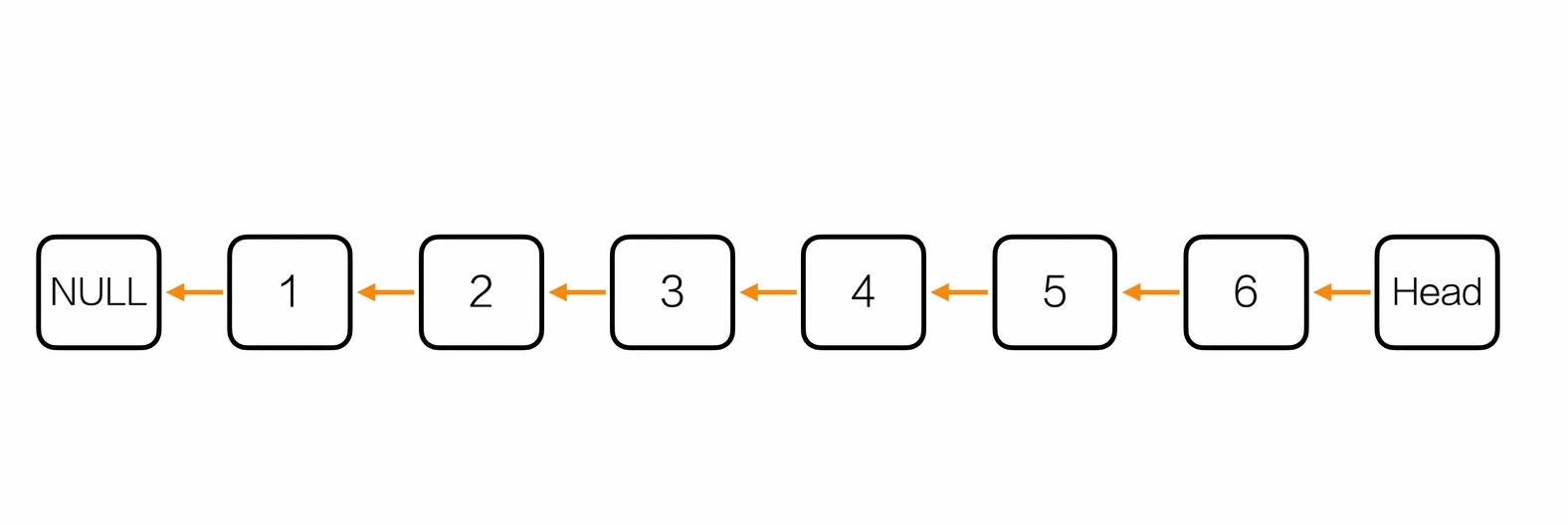
反转链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
| #include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <time.h>
#include <ctype.h>
typedef int ElemType;
typedef struct node{
ElemType data;
struct node * next;
}Node;
Node * InitList(){
Node * link = (Node *)malloc(sizeof(Node));
link->data = 0;
link->next = NULL;
return link;
}
Node * get_tail(Node * L){
Node * p = L;
while(p->next != NULL){
p = p->next;
}
return p;
}
Node * insertTail(Node * tail, ElemType e){
Node * p = (Node *)malloc(sizeof(Node));
p->data = e;
tail->next = p;
p->next = NULL;
return p;
}
Node * reverseList(Node *head){
Node *first = NULL;
Node *second = head->next;
Node *third;
while(second != NULL){
third = second->next;
second->next = first;
first = second;
second = third;
}
Node * hd = InitList();
hd->next = first;
return hd;
}
void freeList(Node * L){
Node * p = L->next;
Node * q;
while(p !=NULL){
q = p->next;
free(p);
p = q;
}
L->next = NULL;
}
void printlistNode(Node * L){
Node * p = L->next;
while(p != NULL){
printf("%d -> ", p->data);
p = p->next;
}
printf("NULL\n");
}
int main(int argc, char const *argv[])
{
Node * list = InitList();
Node * tail = get_tail(list);
for (int i = 1; i <= 7; ++i){
tail = insertTail(tail, i);
}
printlistNode(list);
Node *reverse = reverseList(list);
printlistNode(reverse);
freeList(list);
printlistNode(list);
return 0;
}
|
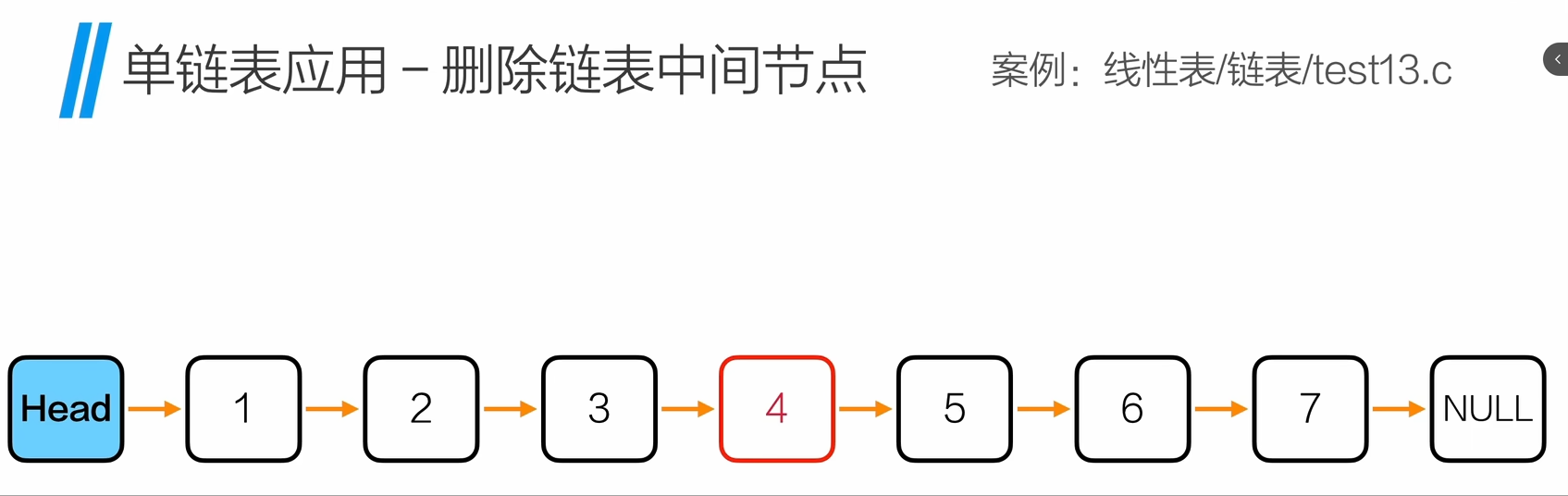
删除中间节点
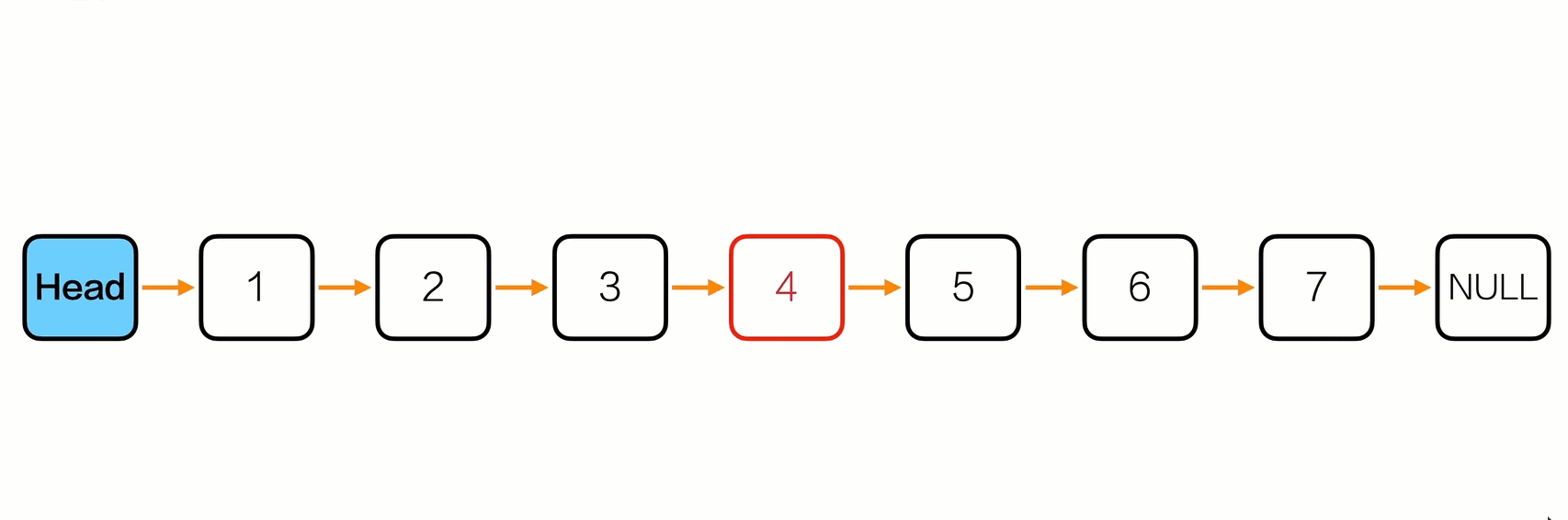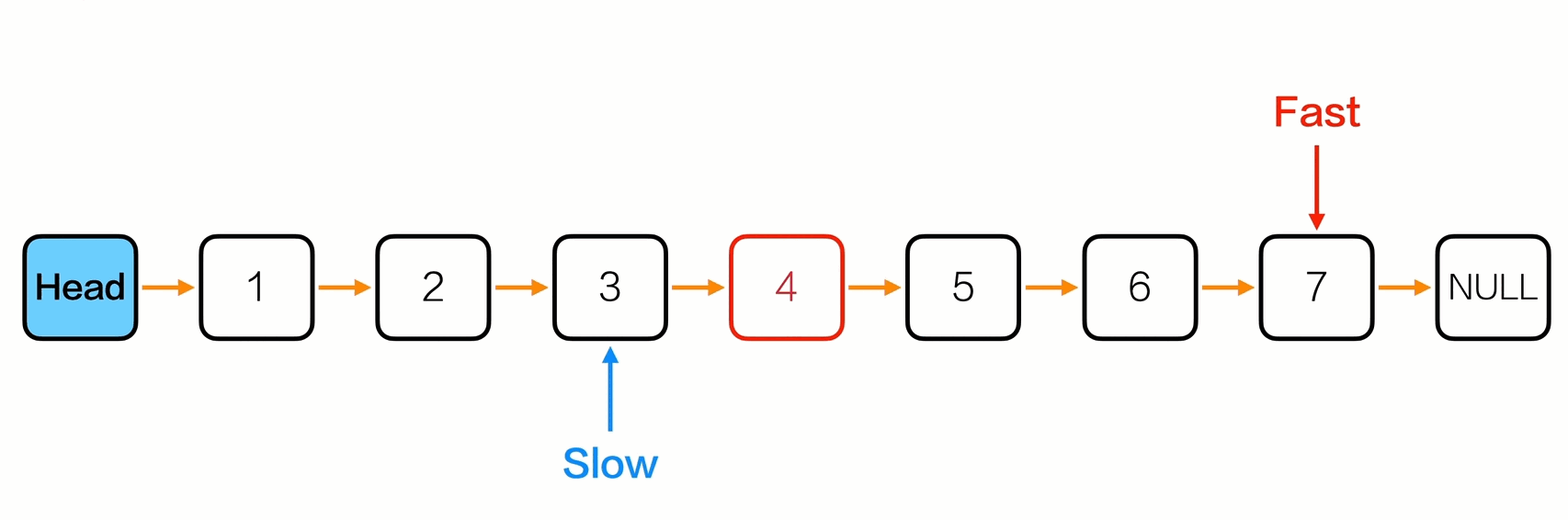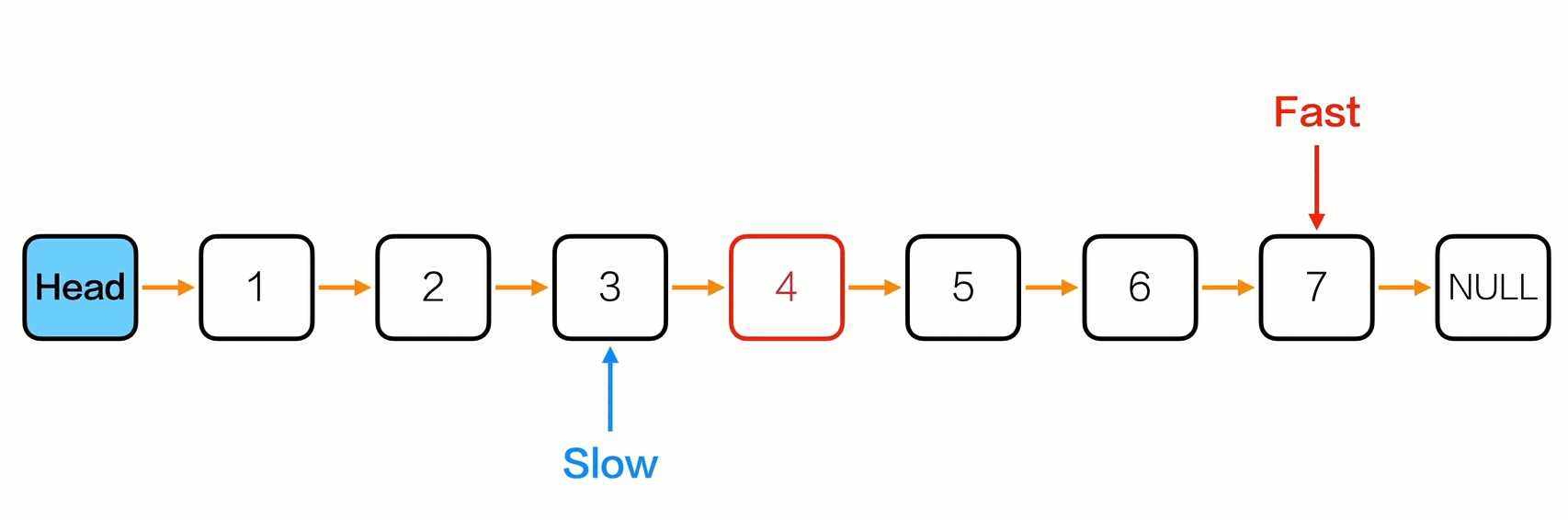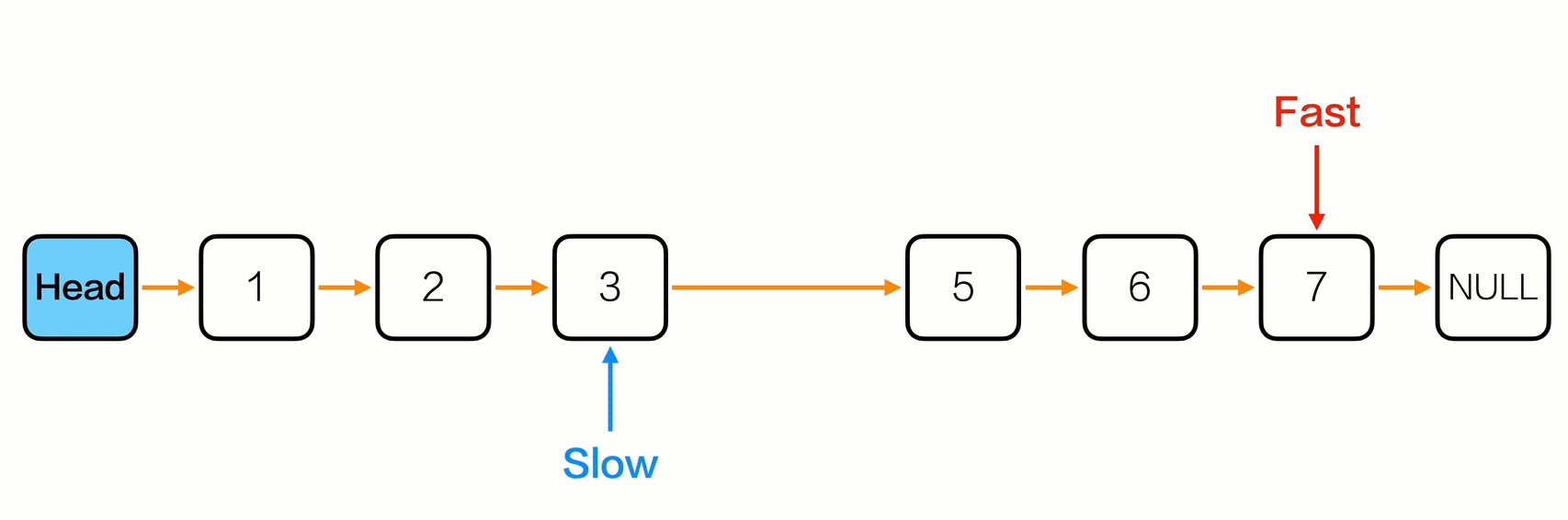
1
2
3
4
5
6
7
8
9
10
11
12
13
|
int delMiddleNode(Node *head){
Node *fast = head->next;
Node *slow = head;
while(fast != NULL && fast->next != NULL){
fast = fast->next->next;
slow = slow->next;
}
Node *p = slow->next;
slow->next = p->next;
free(p);
return 1;
}
|
重新排序

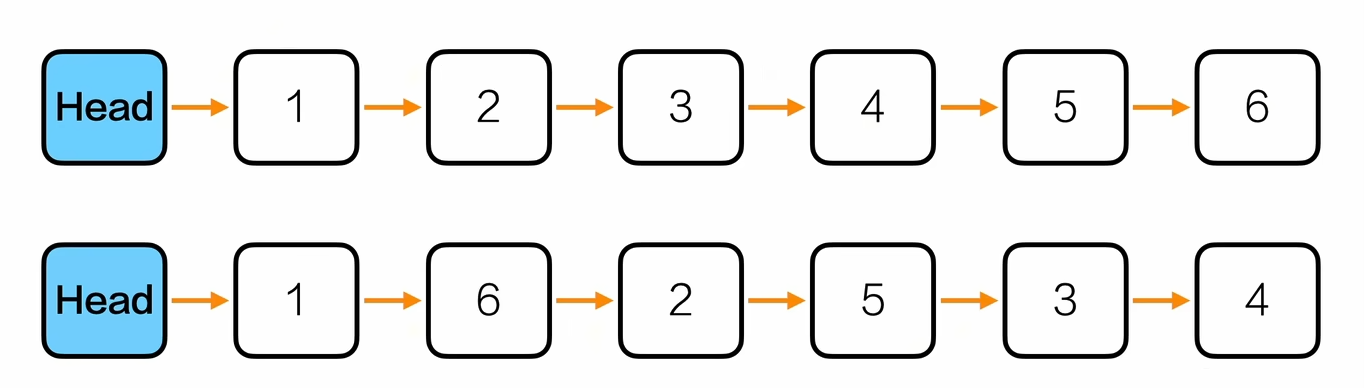
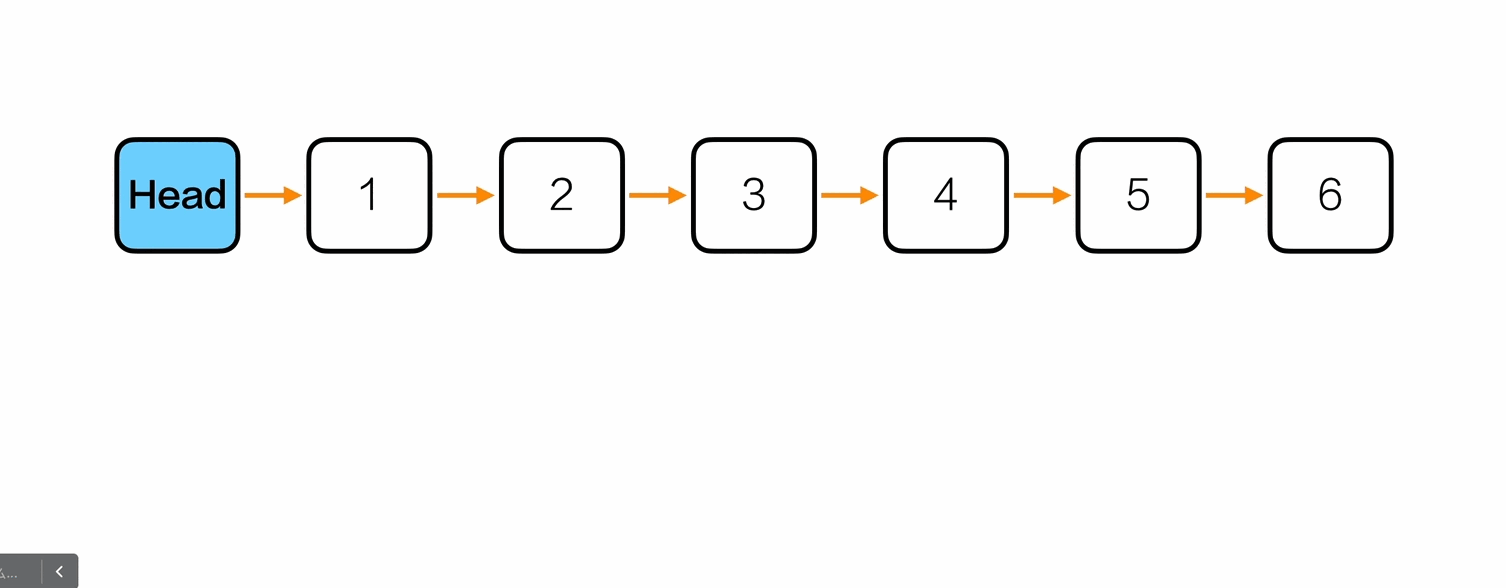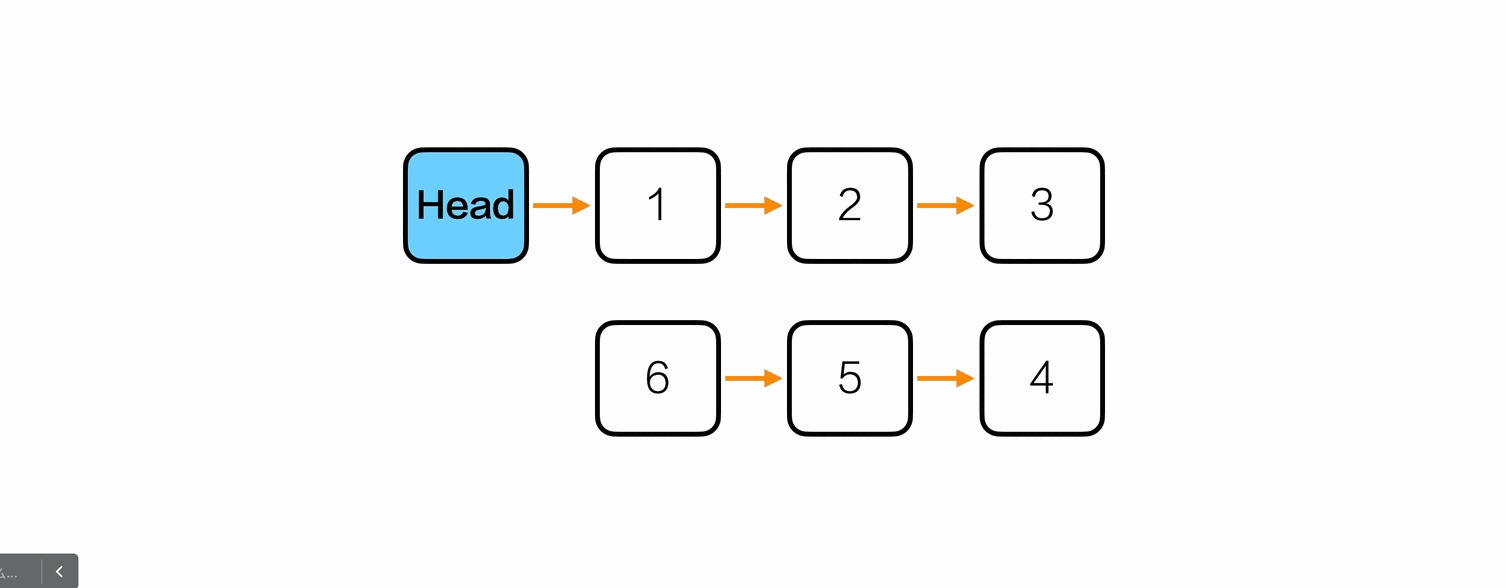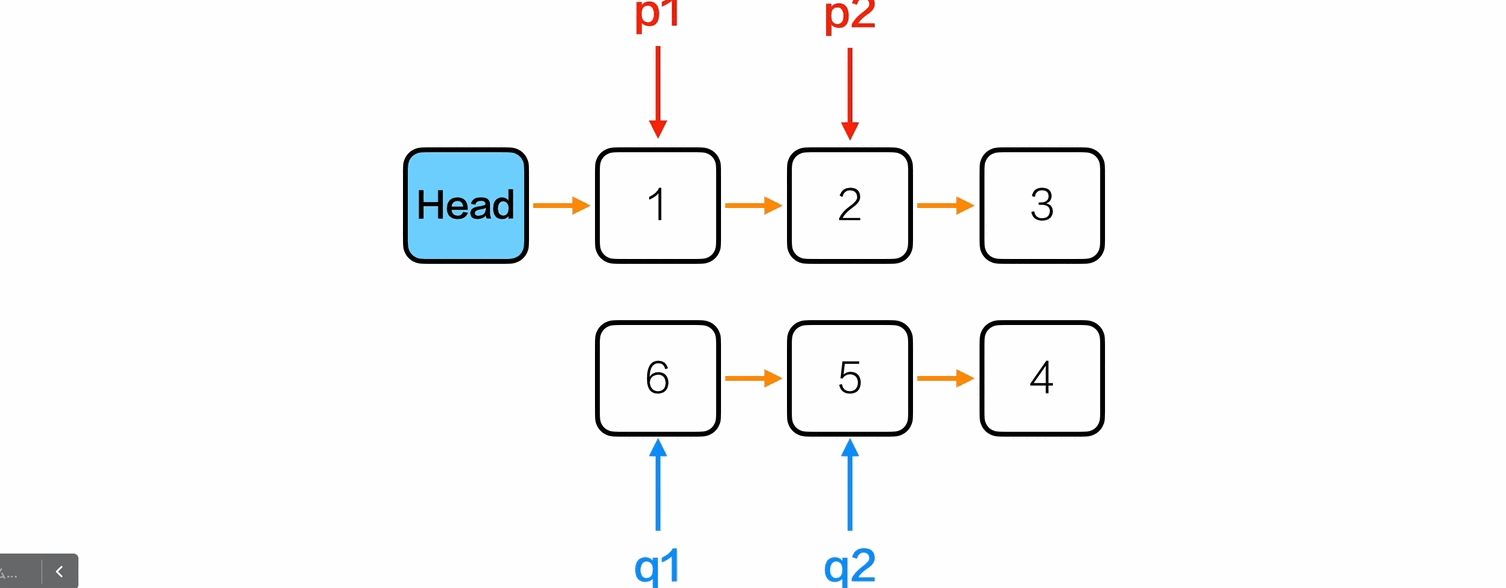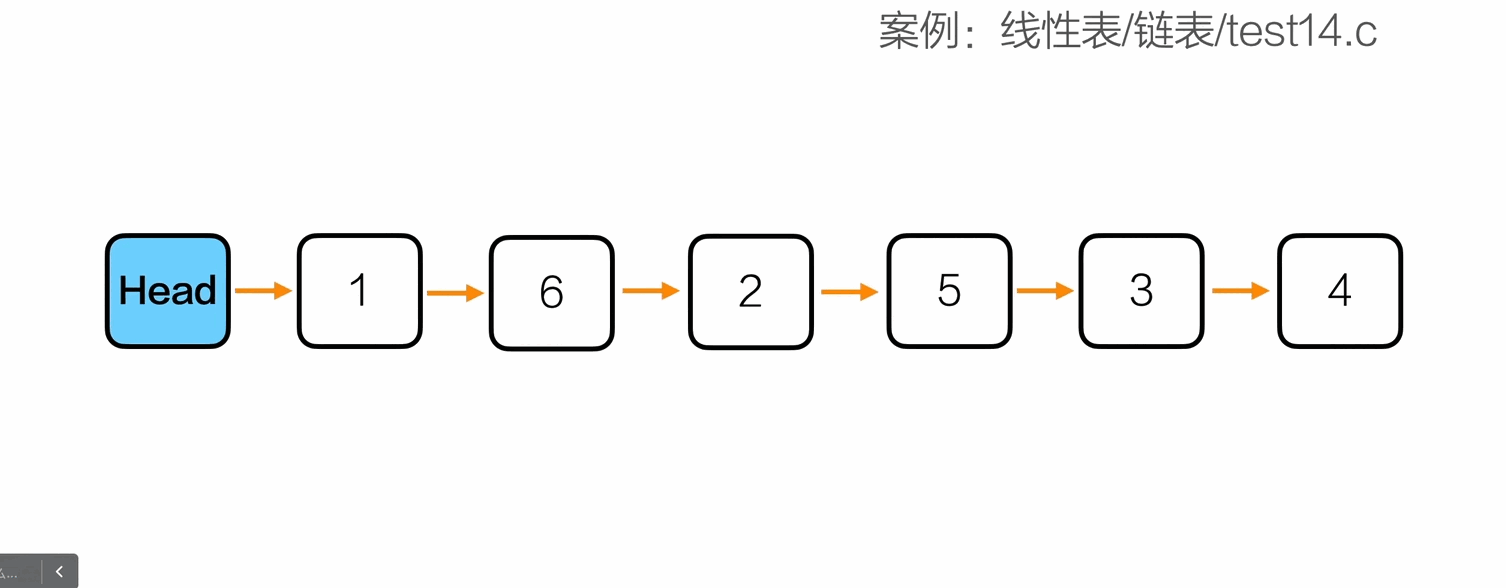
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
void reOrderList(Node *head){
Node *fast = head->next;
Node *slow = head;
while(fast != NULL && fast->next != NULL){
fast = fast->next->next;
slow = slow->next;
}
Node *first = NULL;
Node *second = slow->next;
slow->next = NULL;
Node *third;
while(second != NULL){
third = second->next;
second->next = first;
first = second;
second = third;
}
Node *p1 = head->next;
Node *q1 = first;
Node *p2, *q2;
while(p1 != NULL && q1 != NULL){
p2 = p1->next;
q2 = q1->next;
p1->next = q1;
if(p2 == NULL) break;
q1->next = p2;
q1->next = p2;
p1 = p2;
q1 = q2;
}
}
|
slow->next = NULL; 不断开会发生这个
1
2
3
| 1 -> 6 -> 2 -> 5 -> 3 -> 4
↑ ↓
← ← ← ←
|
if(p2 == NULL) break; // p1 是最后一个,避免 q1->next = p2 出错 如果不做判断,奇数个会因为判断错误,少中间一个元素
链表题
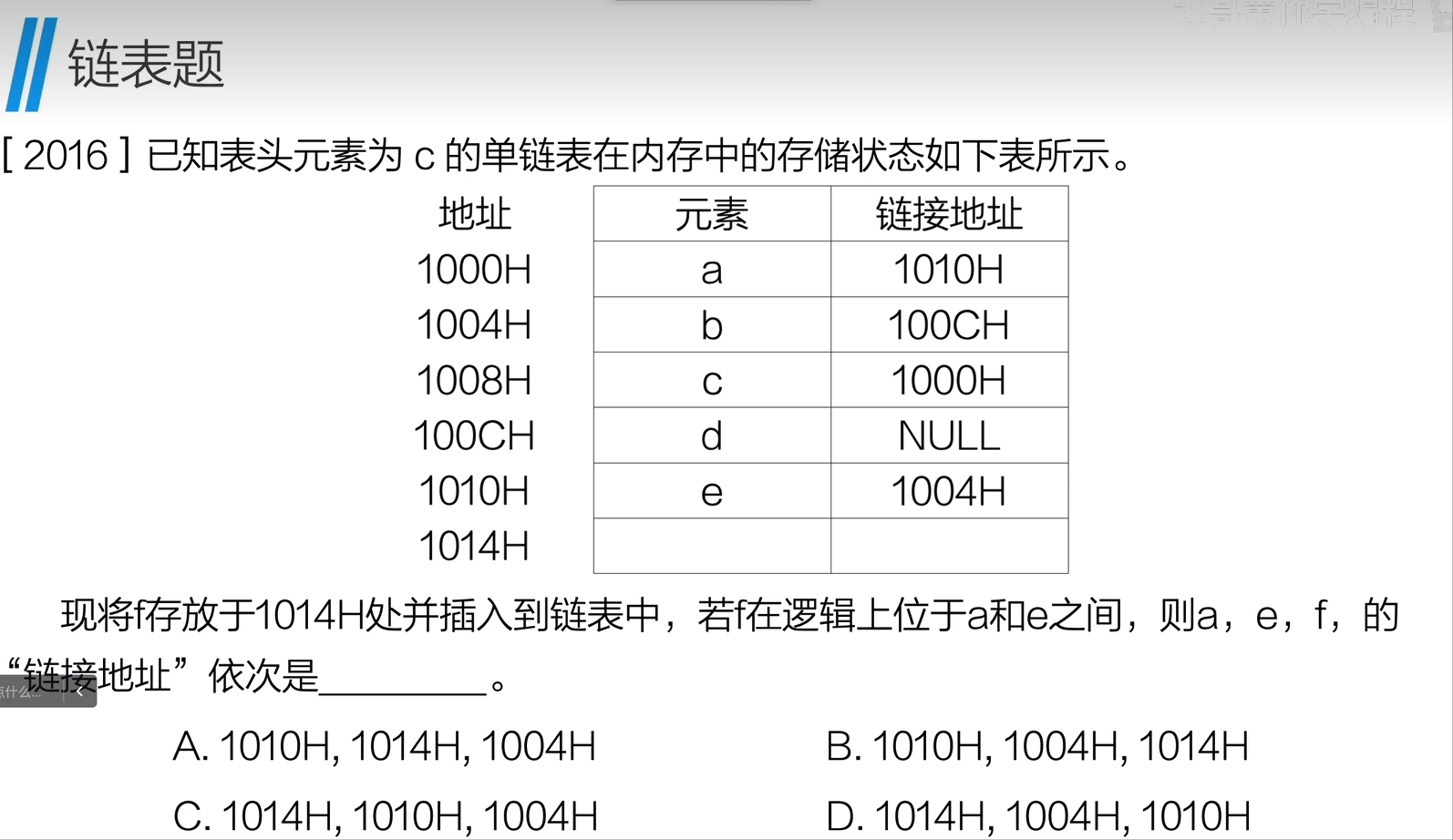
D


D


D

如果是两个节点,那么p作为尾节点就要指向h了,因为等会free(q)后p原本指向的尾节点就没了,p就要指向新的尾节点即h了





































