发表更新算法11 分钟读完 (大约1671个字)  次访问

顺序表

顺序表表示与实现

线性表

定义与特点

定义：由 \(n(n>=0)\) 个数据特性相同的元素构成的有限序列，称为线性表。

线性表是 \(n(n>=0)\) 个数据元素的有限序列，其中 \(n\) 个数据是相同数据类型的。

  • 存在唯一的一个被称作“第一个”的数据元素;

  • 存在唯一的一个被称作“最后一个”的数据元素;

  • 除第一个元素外，结构中的每个数据元素均只有一个前驱;

  • 除最后一个元素外，结构中的每个数据元素均只有一个后继。

线性表ADT

1
2
3
4
5
6
7
8
9
10
11
ADT List {
    数据对象：D={a_i | a_i ∈ ElemSet, i=1,2,…,n, n≥0}
    数据关系：S={<a_{i-1},a_i> | a_{i-1},a_i ∈ D, i=2,…,n}
    基本操作：
        InitList(&L)
        操作结果：构造一个空的线性表L。
        DestroyList(&L)
        初始条件：线性表L已存在。
        操作结果：销毁线性表L。
        ……
} ADT List

顺序表示与实现

用一组连续的内存单元依次存储线性表的各个元素，也就是说，逻辑上相邻的元素，实际的物理存储空间也是连续的。

1
2
3
4
5
6
7
#define MAXSIZE 100
typedef int ElemType;
        
typedef struct SeqList{
    ElemType data[MAXSIZE];
    int length;
}SeqList;
\(a_1\)\(a_2\)...\(a_n\)......
[0][1][n-1][MAXSIZE-1]

初始化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAXSIZE 100
typedef int ElemType;
        
typedef struct SeqList{
    ElemType data[MAXSIZE]; //用静态数组表示顺序表
    int length; //定义数组长度 
}SeqList;

void InitList(SeqList * L){
    //SeqList * L = (SeqList *)malloc(sizeof(SeqList));
    L->length = 0;  
} 

int main(int argc, char const *argv[])
{
    SeqList L;  // 在栈中的内存
    InitList(&L);   // 传入L的地址，初始化 
    printf("初始化成功，目前长度占用%d\n", (&L)->length);
    printf("初始化成功，目前长度占用%d\n", L.length);
    printf("目前占用内存 %zu 字节\n", sizeof(L.data));
    return 0;
}

对指针理解不深刻写出下面代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAXSIZE 100
typedef int ElemType;
        
typedef struct SeqList{
    ElemType data[MAXSIZE]; //用静态数组表示顺序表
    int length; //定义数组长度 
}SeqList;

void InitList(SeqList ** L){	// SeqList **L，通过解引用修改指针。
    *L = (SeqList *)malloc(sizeof(SeqList));	// 堆内存
    (*L)->length = 0;  
} 

int main(int argc, char const *argv[])
{
    SeqList * L;  // 在栈中的内存
    InitList(&L);   // 传入L的地址，初始化 
    printf("初始化成功，目前长度占用 %d\n", L->length);
    //printf("初始化成功，目前长度占用%d\n", L.length);
    printf("目前占用内存 %zu 字节\n", sizeof(L->data));
    return 0;
}
  • 堆内存：是动态分配的内存，程序运行时通过 malloc 或 calloc 等函数向操作系统申请。这部分内存的生命周期由程序员控制，直到通过 free 函数显式释放为止。如果不释放，会导致内存泄漏。
  • 栈内存：内存分配和回收速度非常快，但有大小限制，通常是有限的（受操作系统和硬件的影响）。栈空间是为每个线程分配的，且由系统自动管理。

比较堆和栈内存

  • 栈内存：
    • 自动管理：当函数返回时，栈上分配的内存会自动回收。
    • 空间较小：通常有栈大小限制，一旦超出栈空间就会出现栈溢出错误。
    • 局部作用域：仅在函数内部有效，函数执行完毕后即被销毁。
  • 堆内存：
    • 手动管理：需要程序员显式调用 malloc 申请内存，并用 free 来释放。
    • 空间较大：堆空间通常较大，适合分配较大的数据结构或动态长度的数据。
    • 生命周期由程序员控制：只要你不显式释放，内存就不会被回收，可能导致内存泄漏。

增加元素

1
2
3
4
5
6
7
8
9
int addpendElem(SeqList * L, ElemType e){
    if(L->length == MAXSIZE){
        printf("顺序表已满\n");
        return 0;
    }
    L->data[L->length] = e;
    L->length++;
    return 1;
}

遍历

1
2
3
4
5
6
// 遍历顺序表
void printlistElem(SeqList * L){
    for (int i = 0; i < L->length; ++i){
        printf("顺序表里的元素有：%d \n", L->data[i]);
    }
}

插入元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 指定位置插入元素
int insertElem(SeqList * L, int index, ElemType e){
    if(L->length>=MAXSIZE){
        printf("顺序表当前存储的元素已达到最大值，不能插入\n");
        return 0;
    }
    if(index < 0 || index >= L->length){
        printf("插入的位置不符合顺序表，不能插入\n");
        return 0;
    }
    if(index <= L->length){
        for(int i = L->length -1; i>=index-1; i--){
            L->data[i+1] = L->data[i];
        }
        L->data[index - 1] = e;
        L->length++;
    }
    return 1;
}

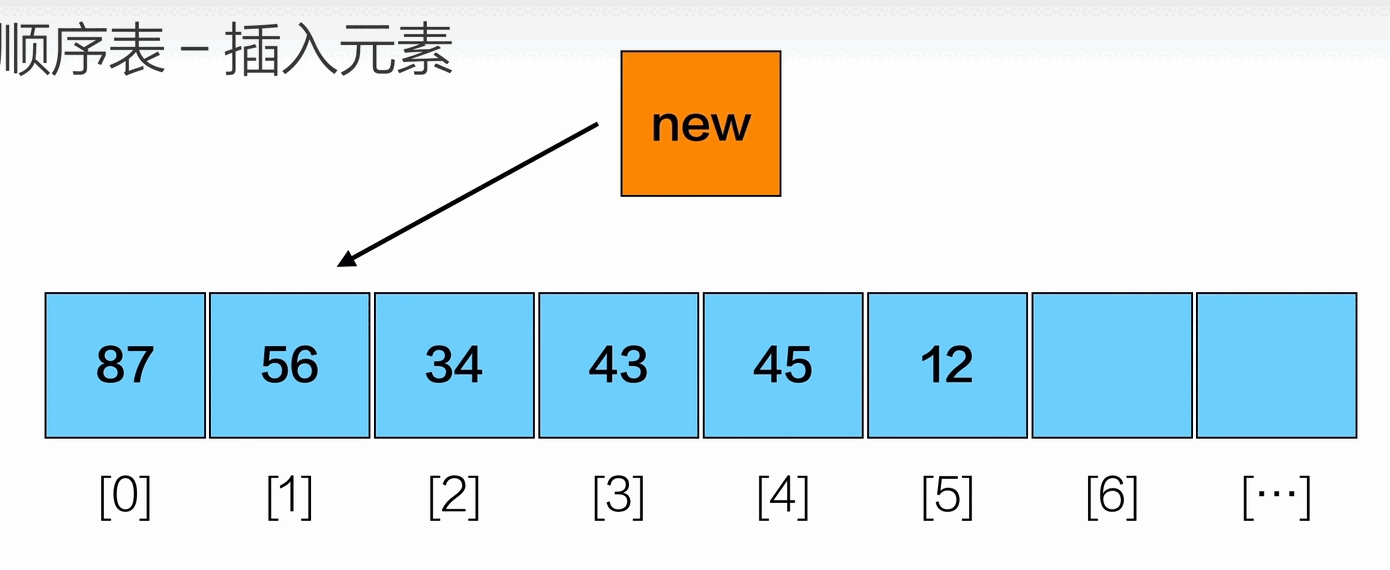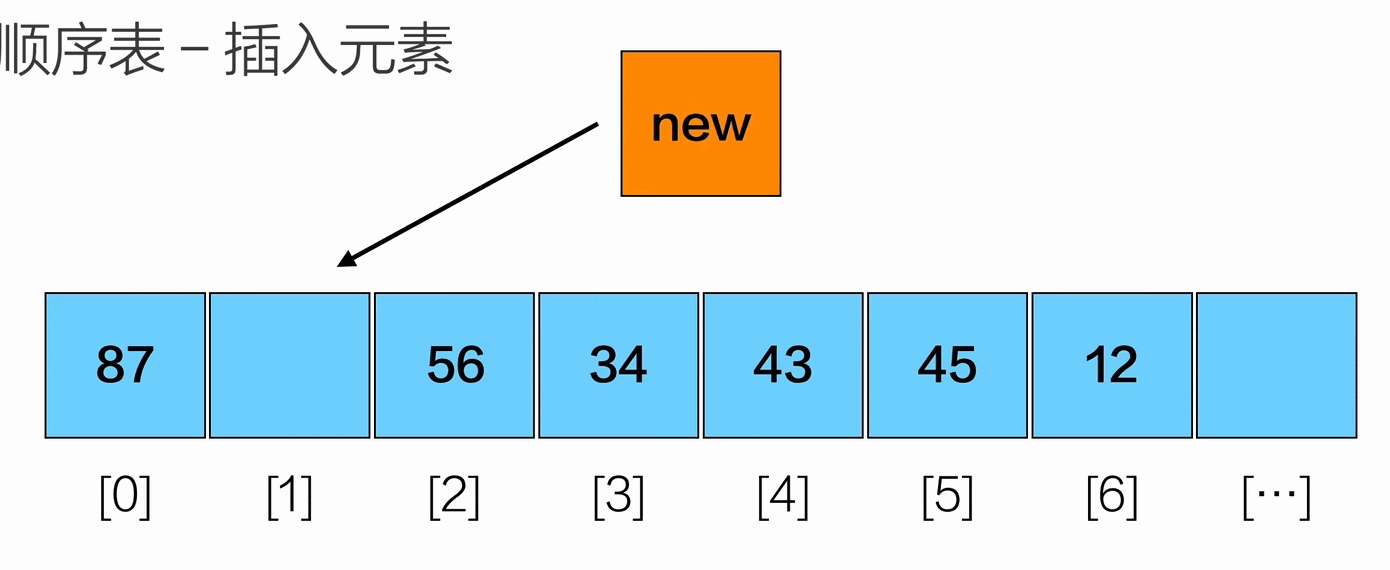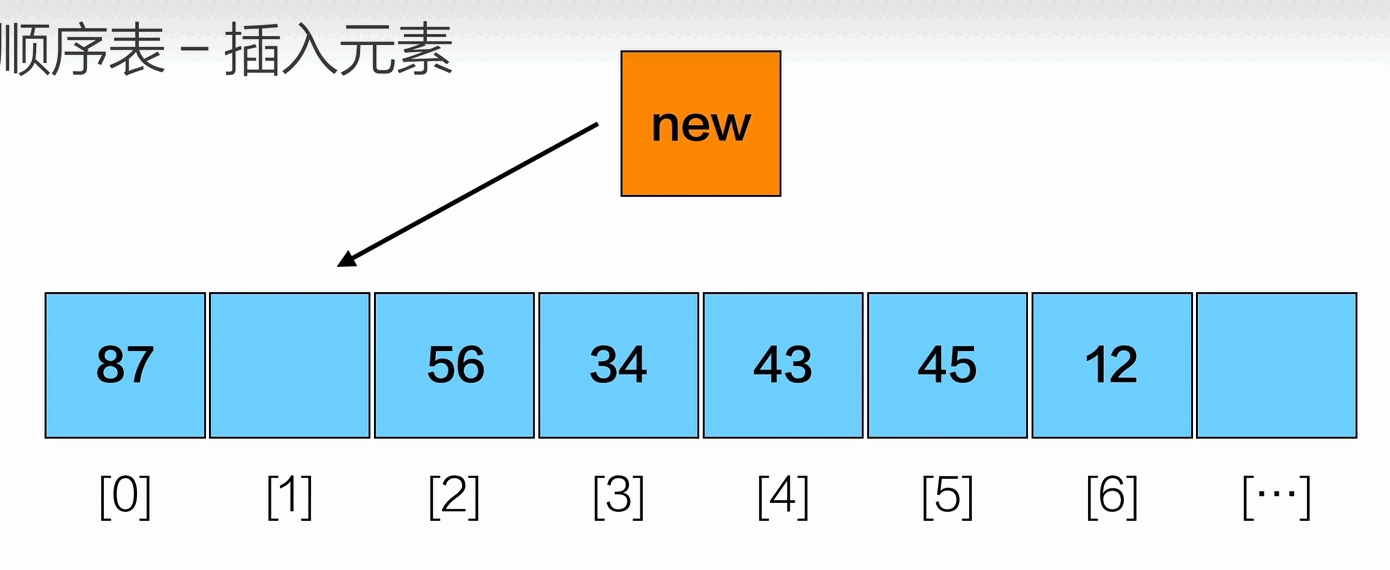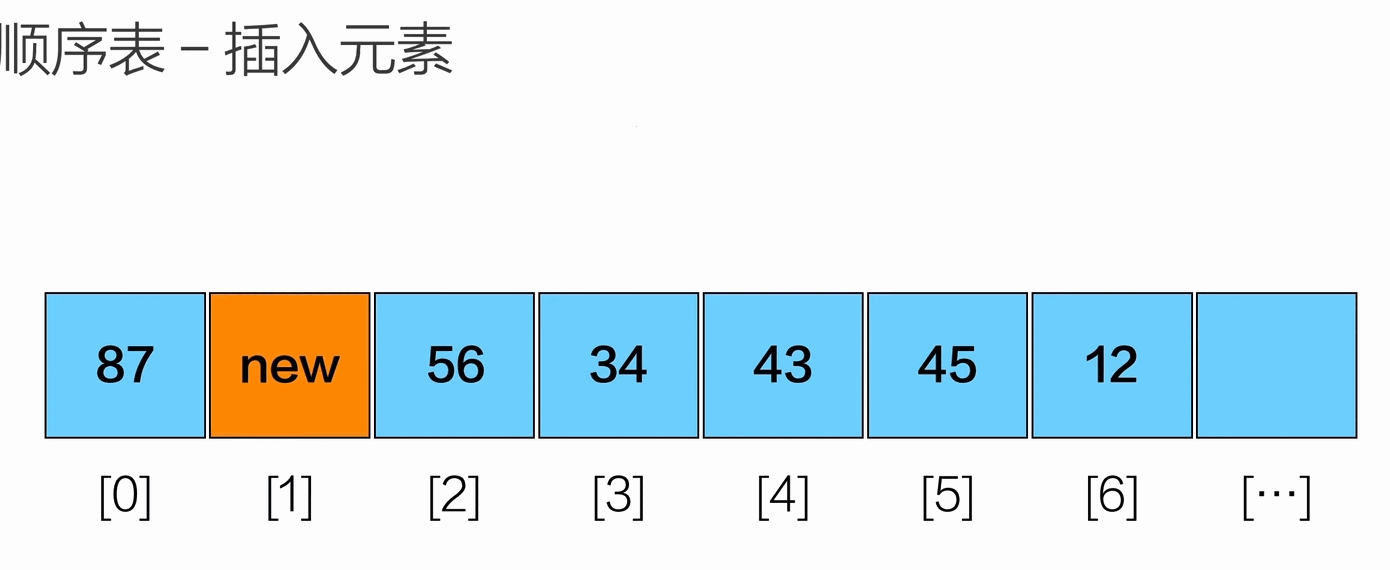
删除元素

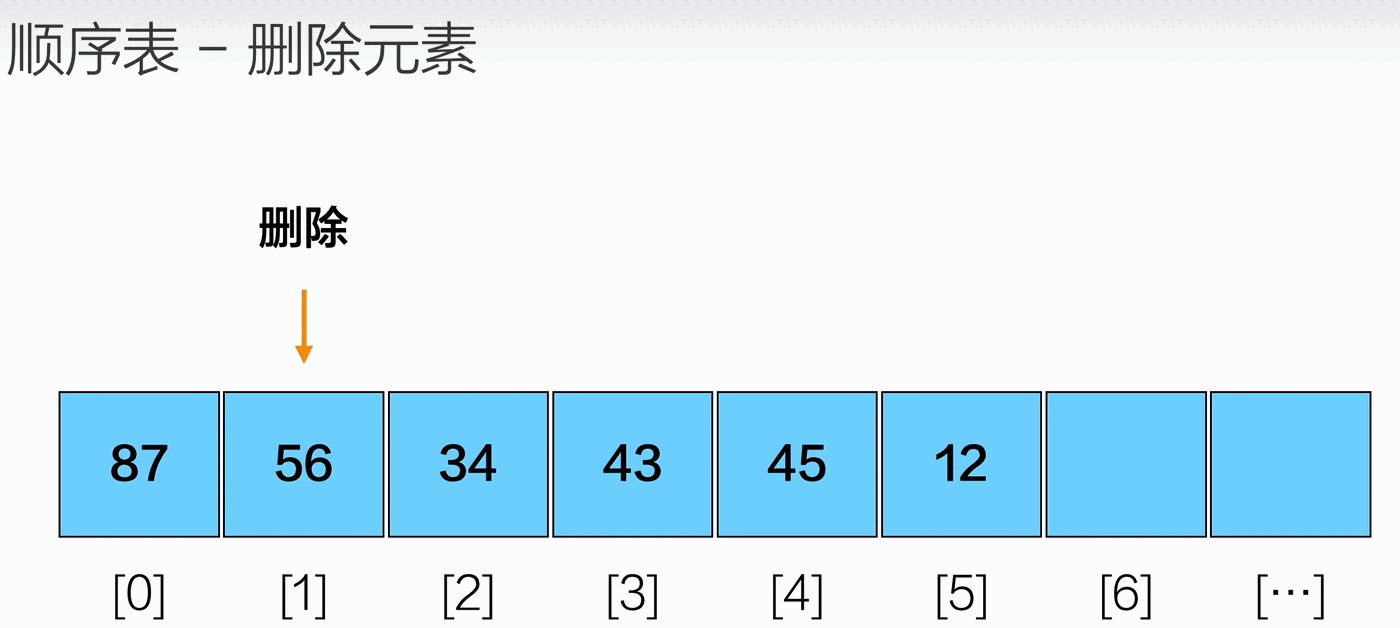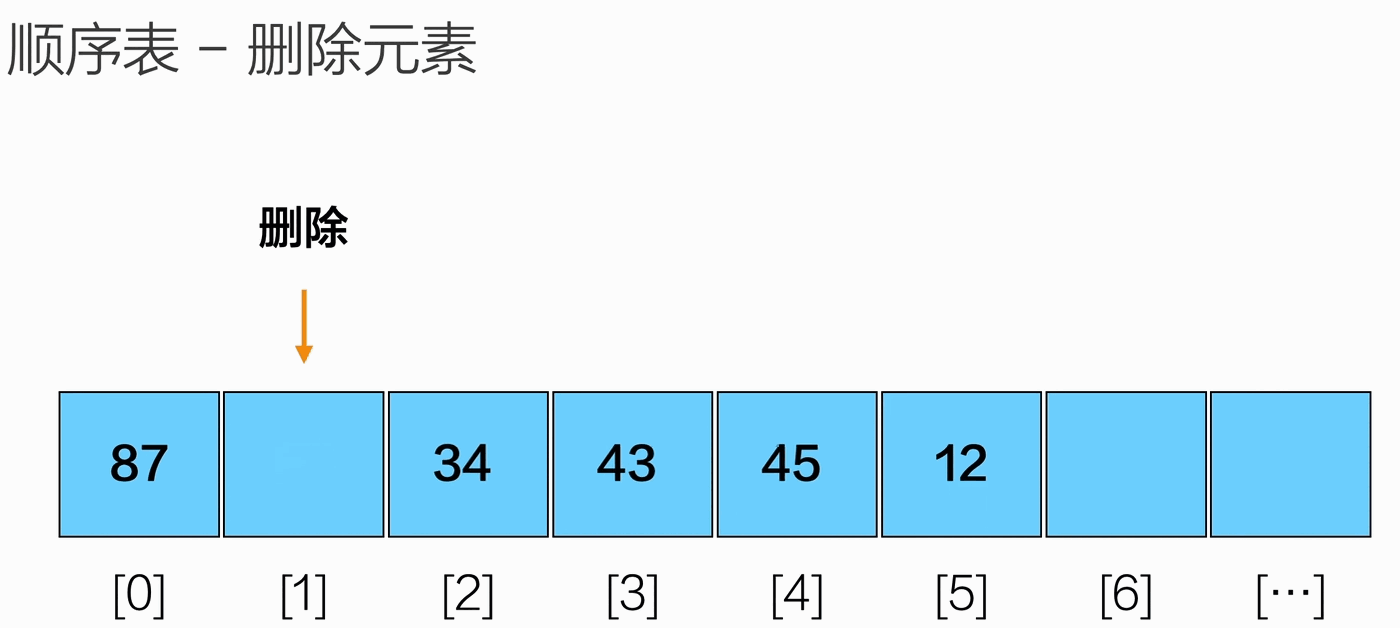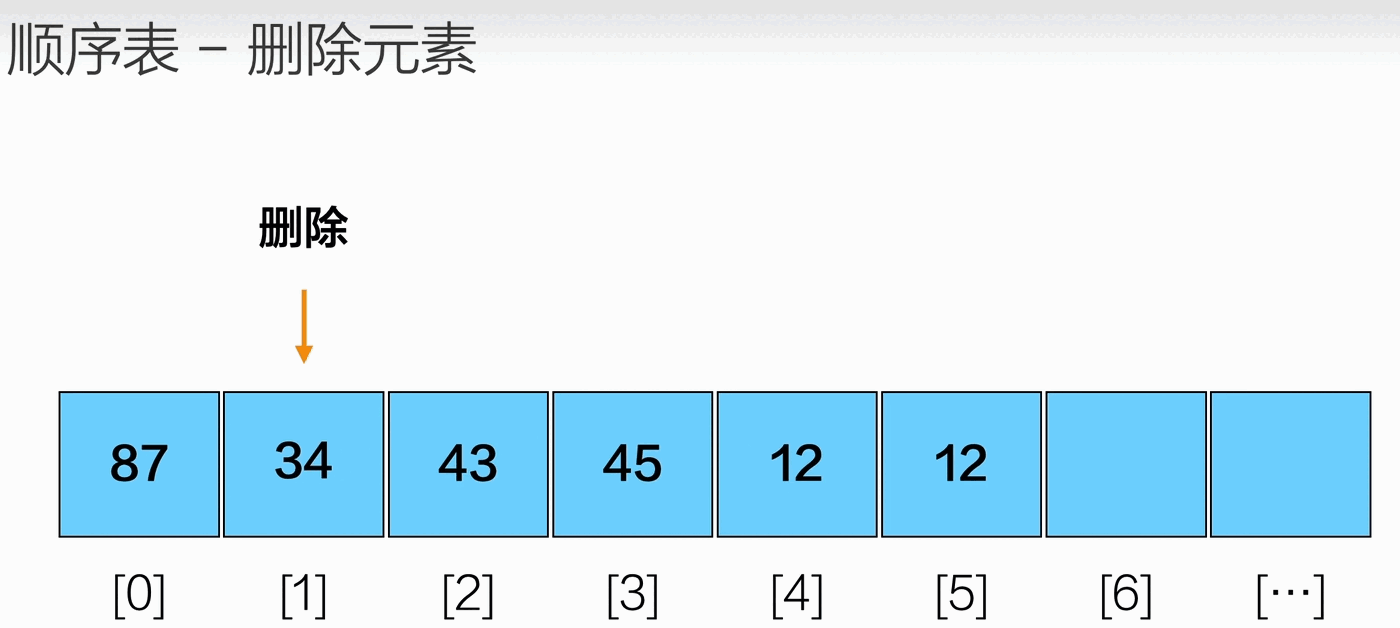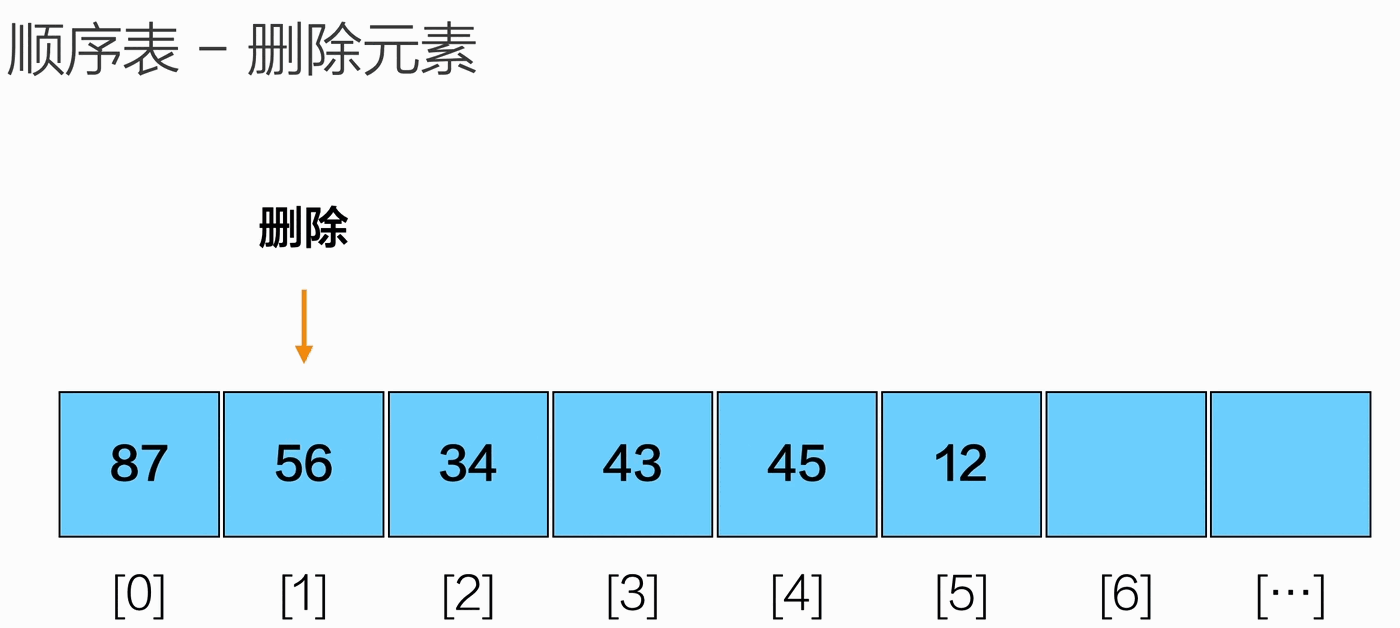
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 删除指定位置元素，传入ElemType * e为返回值
int deleteElem(SeqList * L, int index, ElemType * e){
    if(L->length <= 0){
        printf("顺序表元素为空，不能删除\n");
        return 0;
    }
    if(index < 0 || index >= L->length){
        printf("删除的位置不符合顺序表，不能删除\n");
        return 0;
    }
    *e = L->data[index-1];  // 存储删除的数据
    if(index < L->length){
        for (int i = index -1; i < L->length; ++i)
        {
            L->data[i] = L->data[i+1];
        }
        L->length--;
        return 1;
    }

}

按值查找

1
2
3
4
5
6
7
8
9
10
11
// 按值查找
int findElem(SeqList * L, ElemType e){
    for(int i = 0; i < L->length; i++){
        if(L->data[i] == e){
            printf("你要查找的元素 %d 在顺序表第 %d 个位置\n", e, i + 1);
            return i + 1;
        }
    }
    printf("未查找到该元素\n");
    return 0;
}

动态分配内存地址初始化

✅ 方法 1：使用静态数组

如果你使用的就是固定大小的数组（如你原来定义的那样）：

1
2
3
4
typedef struct SeqList{
    ElemType data[MAXSIZE]; // 静态数组
    int length;
} SeqList;

就不需要也不能再动态分配 data，所以 InitList 应该改成这样：

1
2
3
4
5
SeqList * InitList(){
    SeqList * L = (SeqList *)malloc(sizeof(SeqList));
    L->length = 0;
    return L;
}

✅ 方法 2：改成指针 + 动态内存分配

如果你真的想动态分配 data，应该把结构体改成：

1
2
3
4
typedef struct SeqList{
    ElemType *data;  // 变成指针
    int length;
} SeqList;
1
2
3
4
5
6
SeqList * InitList(){
    SeqList * L = (SeqList *)malloc(sizeof(SeqList));
    L->data = (ElemType *)malloc(sizeof(ElemType) * MAXSIZE);
    L->length = 0;  
    return L;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
typedef struct SeqList{
    ElemType * data; // ElemType 指针类型的data
    int length; // 定义数组长度 
}SeqList;

// seqlist存放的是data（指针）和length，data指向另一片新开的空间。
SeqList * InitList(){
    //这里声明空间了,但是没有指向,就是个野指针
    SeqList * L = (SeqList *)malloc(sizeof(SeqList));   
    //因为data是指针，结构体分配指针大小空间，而指向的数组需要额外申请
    L->data = (ElemType *)malloc(sizeof(ElemType) * MAXSIZE); //L->data 是指向 堆上另一个数组的指针。
    L->length = 0;  
    return L;
}

问题：

顺序表插入元素的最好时间复杂度是？ \(O(1)\)

顺序表插入元素的最坏时间复杂度是？ \(O(n)\)

线性表的顺序存储形式（顺序表）有哪些点让你觉得很麻烦？插入删除麻烦

顺序表

https://vconlln.cn/shunxubiao.html

作者

Vc0n1ln

发布于

2025-05-28

更新于

2025-05-29

许可协议

CC BY 4.0

#

喜欢这篇文章？打赏一下作者吧

评论

哔哩哔哩 Bilibili

归档

最新文章

标签

Archlinux5
CTF比赛1
Crypto3
blog1
css1
数据结构3
Your browser is out-of-date!

Update your browser to view this website correctly.&npsb;Update my browser now

×

×