2025-06-24发表2025-06-24更新Crypto21 分钟读完 (大约3161个字) 次访问

流密码

参考《现代密码学（第5版）》（杨波编著）

1.流密码基本概念

1.1流密码核心思想

密钥流生成：用密钥 $k$ 生成无限长的密钥流 $z = z_0z_1z_2...$
加密规则：明文 $x=x_0x_1x_2...$ 与密钥流逐位异或：$y = y_0y_1y_2...=E_{z_0}(x_0)E_{z_1}(x_1)E_{z_2}(x_2)...$
动态变化：密钥流由密钥发生器 $f$ 控制，每个密钥位 $z_i = f(k,σ_i)$ 都依赖：

初始密钥 $k$
$i$ 时刻的状态 $σ_i$
$f$ 是密钥 $k$ 和 $σ_i$ 的函数

1.2 关键区别：记忆性

特性	流密码	分组密码
记忆性	有（依赖历史状态）	无
加密过程	逐位加密，密钥流动态变化	固定分组，独立处理每块
影响因素	后续密钥可能受前文影响	每个分组完全独立

💡 类比理解：

流密码像流水线，前面的加密结果会影响后面
分组密码像切片机，每一块独立处理，互不影响

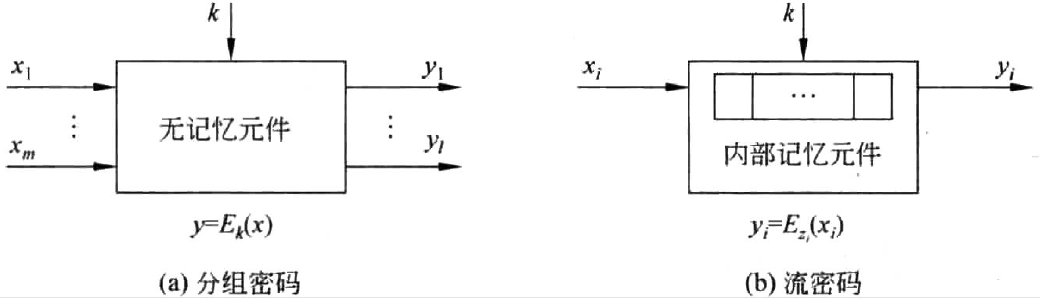
1.3 同步流密码（精简版）

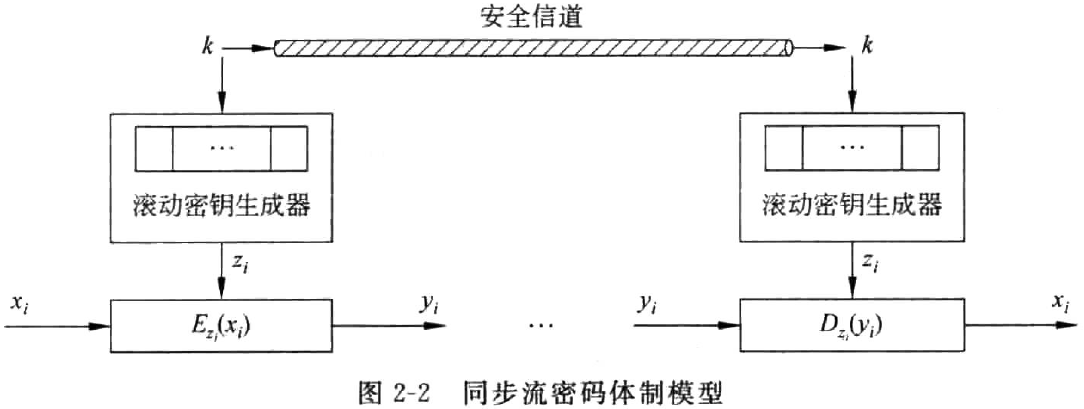
同步流密码特点:

模型结构
- 密钥流生成器：独立生成密钥流 $z_i = f(k, σ_i)$
- 加密变换器：对明文 $x_i$ 进行可逆变换 $y_i = E_{z_i}(x_i)$
解密过程
\[ x_i = D_{z_i}(y_i) （与明文历史无关） \]
典型应用

二元加法流密码：最常用形式，加密规则为异或操作：
\[ y_i = z_i ⊕ x_i \]

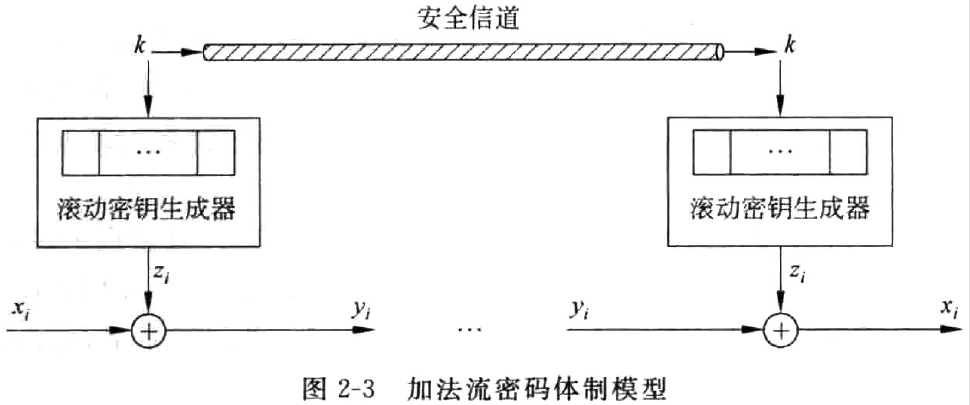
为什么同步流密码更易分析？

密钥流仅由 $k$ 和初始状态 $σ_0$ 决定，与明文无关
解密无需知道前序明文，便于数学建模和安全性分析
大多数理论研究和实际系统（如One-Time Pad）基于此模型

一次一密与流密码关系

一次一密密码是流密码的终极理想形态
📌 当密钥流 $z_i = k_i$（即直接使用原始密钥）时，流密码退化为一次一密密码

密码设计目标

滚动密钥生成器，使得密钥 $k$ 经其扩展成的密钥流序列 $z$ 需满足以下关键特性:

超长周期：密钥流重复前尽可能多生成新密钥
统计随机性：密钥流分布接近完美随机
抗数学攻击：能抵抗线性分析和统计模式识别
不可预测性：即使知道部分密钥流，也无法推断剩余部分

💡 性质：极大的周期、良好的统计特性、抗线性分析、抗统计分析。

1.4 有限状态自动机

定义

有限状态自动机是具有离散输入和输出的数学模型，由三部分构成：

状态集合 $ S = {s_1, s_2, ..., s_l} $
输入字符集 $ A_1 = {A_1^{(1)}, A_2^{(1)}, ..., A_m^{(1)}} $ ，输出字符集 $ A_2 = {A_1^{(2)}, A_2^{(2)}, ..., A_n^{(2)}} $
转移函数

\[ \begin{align*} A_k^{(2)} &= f_1(s_i, A_j^{(1)}) \\ s_h &= f_2(s_i, A_j^{(1)}) \end{align*} \]

即当处于状态 $ s_i $，输入 $ A_j^{(1)} $ 时：
➡️ 输出 $ A_k^{(2)} $
➡️ 状态迁移至 $ s_h $

示例:

以具体实例理解结构:

状态集合：$ S = {s_1, s_2, s_3} $
输入字符集：$ A_1 = {A_1^{(1)}, A_2^{(1)}, A_3^{(1)}} $
输出字符集：$ A_2 = {A_1^{(2)}, A_2^{(2)}, A_3^{(2)}} $
转移函数：由表2-1定义

用转移图可视化自动机行为

顶点：代表不同状态（如 $ s_1, s_2, s_3 $）
有向弧线：从状态 $ s_i $ 到 $ s_j $ 的箭头，标注输入/输出对 $ (A_i^{(1)}, A_j^{(2)}) $
示例：见图2-4

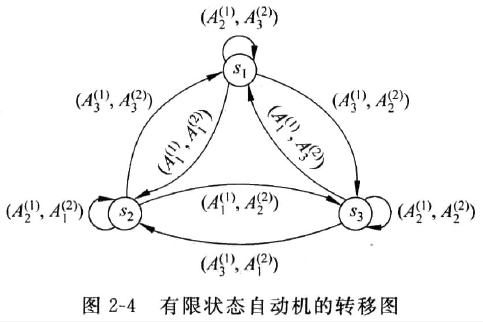
若输入序列为 $A_1^{(1)}A_2^{(1)}A_1^{(1)}A_3^{(1)}A_3^{(1)}A_1^{(1)}$ 初始状态为 $s_1$ ，得到状态序列 $s_1s_2s_2s_3s_2s_1s_2$ 输出字符序列为 $A_1^{(2)}A_1^{(2)}A_2^{(2)}A_1^{(2)}A_3^{(2)}A_1^{(2)}$

💡 关键特性：
自动机的行为完全由当前状态和输入决定，输出与未来状态均通过转移函数唯一确定

1.5 密钥流产生器

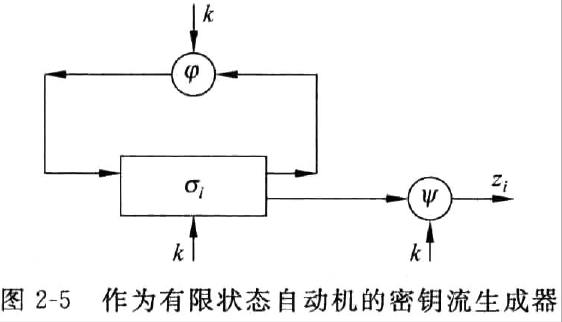
同步流密码的安全性完全依赖于密钥流生成器的设计，它本质上是一个状态机模型。

组成要素

密钥流生成器包含四部分

输出符号集 $ Z $：密钥流的可能取值范围
状态集合 $ $：记录加密过程的不同阶段
状态转移函数 $ $：
\[ 当前状态 σ_i → 下一状态 σ_{i+1} \]
输出函数 $\psi$ ：

\[ 当前状态σ_i → 当前密钥 z_i \;(输出符号集) \]

初始状态 $σ_0$

设计目标

输出要求：生成的密钥流 $z=z_0z_1z_2... $ 需满足：

超长周期（不重复）
统计随机性
抗攻击性（抵抗线性/统计分析）

实现要求：

状态转移函数 $ $ 和输出函数 $\psi$ 使得输出序列满足要求
硬件/软件实现简单
资源消耗低

非线性状态转移（$ $ ）的自动机理论不成熟，导致：
- 分析工具匮乏
- 性能预测困难
解决方案：采用「线性 $ $ + 非线性组合 $\psi$ 」架构：
\[ 线性 \varphi → 易分析的状态转移 \\ 非线性 \varphi → 强化输出序列安全性 \]

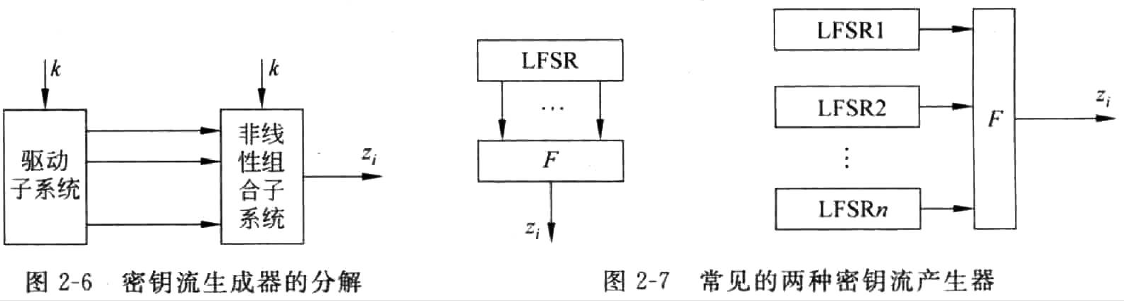
驱动部分 + 非线性组合部分 （图2-6），目前最流行的方案（见图2-7）：

驱动部分：线性反馈移位寄存器（LFSR）控制生成器的状态转移，并为非线性组合部分提供统计性能好的序列。

非线性组合部分：利用这些序列组合出满足要求的密钥流序列。

2. 线性反馈移位寄存器（LFSR）

2.1 定义

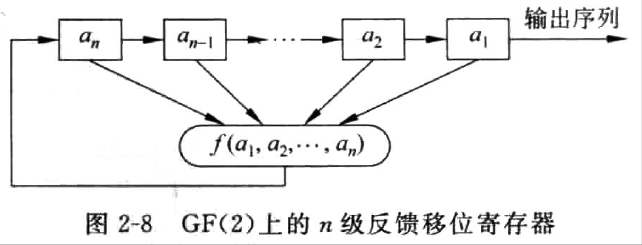
线性反馈移位寄存器是流密码中生成密钥流的核心组件，$GF(2)$ 上一个 $n$ 级反馈移位寄存器由两部分构成：

n级存储单元：$n$ 个二元存储器，每个单元保存 $1$ 位二进制数据（0或1）
反馈函数 $ f(a_1, a_2, ..., a_n) $：是 $n$ 元布尔函数，即 $n$ 个变元 $a_1, a_2, \ldots, a_n$ 可以独立地取 $0$ 和 $1$ 这两个可能的值，函数中的运算有逻辑与、逻辑或、逻辑补等运算，最后的函数值也为 $0$ 或 $1$。

2.2 工作原理

状态表示

每个时刻，寄存器的状态是一个 $n$ 位二进制序列： $(a_1, a_2, ..., a_n)$
总共有 $2^n$种可能状态 （类似掷n次硬币的所有结果）
$a_i$ 是第 $i$ 级存储器的内容

数据流动

初始状态由用户确定，当第 $i$ 个移位脉冲到来时，每一级存储器 $a_i$ 都将其内容向下一级 $a_{i-1}$ 传递，

钟脉冲触发：每接收一次时钟信号：
- 每个存储单元将当前值传递给下一级
- 最高位根据寄存器此时的状态 $a_1, a_2, \ldots, a_n$ 计算 $f(a_1, a_2, \ldots, a_n)$，作为下一时刻的 $a_n$
反馈函数规则：
- 输入：当前所有存储单元的值 $(a_1, a_2, ..., a_n)$
- 输出：通过 逻辑与/或/异或 运算生成新值（0或1）

例如：

图是一个3级反馈移位寄存器，其初始状态为 $(a_1,a_2,a_3)=(1,0,1)$

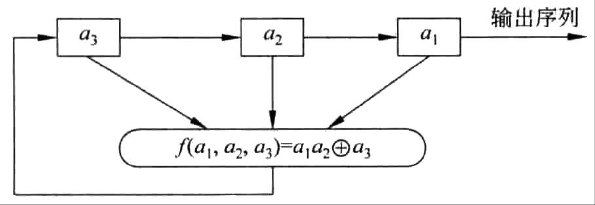
输出由表得，输出序列1011 1011 1011...，周期为4

如果移位寄存器的反馈函数 $ f(a_1, a_2, ..., a_n) $ 是 $a_1,a_2,...,a_n$ 的线性函数，则称之为线性反馈移位寄存器(LFSR)，此时 $f$ 可以写为： \[ f(a_1, a_2, ..., a_n) = c_na_1 \oplus c_{n-1}a_2 \oplus... \oplus c_1a_n \] 其中常数 $c_i = 0 或 1$ ，$\oplus$ 是模 $2$ 加法。$c_i = 0或1$ 可以用开关的断开和闭合来实现

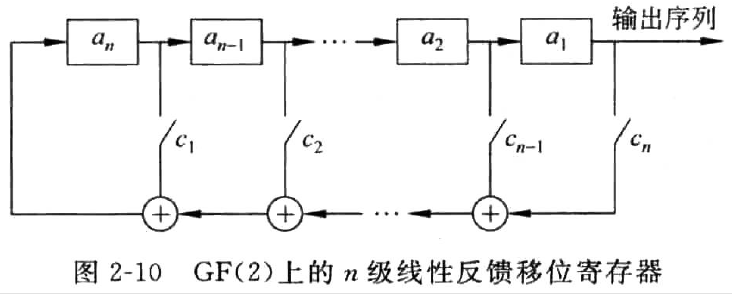
输出序列 $\{a_t\}$ 满足如下式子，其中 $t$ 为非负正整数。 \[ a_{n+t} = c_na_t \oplus c_{n-1}a_{t+1} \oplus... \oplus c_1a_{n+t-1} \] 线性反馈移位寄存器因其实现简单、速度快、有较为成熟的理论等优点而成为构造密钥流生成器的最重要的部件之一。

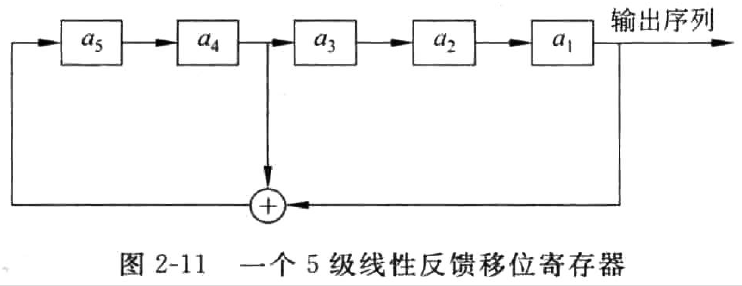
例

图2-11是一个 $5$ 级线性反馈移位寄存器，其初始状态为 $(a_1, a_2, a_3, a_4, a_5) = (1, 0, 0, 1, 1)$，可求出输出序列为
\[ 10011010010000101011101111100110\ldots \] 周期为31。

在线性反馈移位寄存器中总是假定 $c_1, c_2, \ldots, c_n$ 中至少有一个不为0，否则 $f(a_1, a_2, \ldots, a_n) \equiv 0$，这样的话，在 $n$ 个脉冲后状态必然是 $00\ldots0$，且这个状态必将一直持续下去。若只有一个系数不为0，设仅有 $c_j$ 不为0，实际上是一种延迟装置。

一般对于 $n$ 级线性反馈移位寄存器，若反馈函数为线性组合，则其输出序列的周期 最多为 $2^n - 1$。

线性反馈移位寄存器的性质

线性反馈移位寄存器输出序列的性质完全由其反馈函数决定。
$n$ 级线性反馈移位寄存器最多有 $2^n$ 个不同的状态。
若其初始状态为 $0$，则其状态恒为 $0$。
若其初始状态非 $0$，则其后继状态不会为 $0$。
因此 $n$ 级线性反馈移位寄存器的状态周期小于等于 $2^n - 1$。
其输出序列的周期与状态周期相等，也小于等于 $2^n - 1$。
只要选择合适的反馈函数便可使序列的周期达到最大值 $2^n - 1$，周期达到最大值的序列称为 $m$ 序列。

2.3 线性移位寄存器的一元多项式表示

设 $n$ 级线性移位寄存器的输出序列 $\{a_i\}$ 满足递推关系
\[ a_{n+k} = c_1 a_{n+k-1} \oplus c_2 a_{n+k-2} \oplus \cdots \oplus c_n a_k \tag{*} \] 对任何 $k \geq 1$ 成立。这种递推关系可用一个一元高次多项式
\[ p(x) = 1 + c_1 x + \cdots + c_{n-1} x^{n-1} + c_n x^n \] 表示，称这个多项式为 LFSR 的特征多项式。

设 $n$ 级线性移位寄存器对应于递推关系 $(*)$，由于 $a_i \in \text{GF}(2) \ (i = 1, 2, \ldots, n)$，所以共有 $2^n$ 组初始状态，即有 $2^n$ 个递推序列，其中非恒零的有 $2^n - 1$ 个，记 $2^n - 1$ 个非零序列的全体为 $G(p(x))$。

隐藏内容的标题

定义2-1

给定序列 $\{a_i\}$，幂级数
\[ A(x) = \sum_{i=1}^{\infty} a_i x^{i-1} \] 称为该序列的生成函数。

定理2-1

设 $p(x) = 1 + c_1 x + \cdots + c_{n-1} x^{n-1} + c_n x^n$ 是 GF(2) 上的多项式，$G(p(x))$ 中任一序列 $\{a_i\}$ 的生成函数 $A(x)$ 满足：
\[ A(x) = \frac{\phi(x)}{p(x)} \] 其中
\[ \phi(x) = \sum_{i=1}^{n} \left( c_{n-i} x^{n-i} \sum_{j=1}^{i} a_j x^{j-1} \right) \]

定理2-2

$p(x) \mid q(x)$ 的充要条件是 $G(p(x)) \subseteq G(q(x))$。

定义2-2

设 $p(x)$ 是 GF(2) 上的多项式，使 $p(x) \mid (x^p - 1)$ 的最小 $p$ 称为 $p(x)$ 的周期或阶。

定理2-3

若序列 $\{a_i\}$ 的特征多项式 $p(x)$ 定义在 GF(2) 上，$p$ 是 $p(x)$ 的周期，则 $\{a_i\}$ 的周期 $r \mid p$。

定义2-3

仅能被非零常数或自身的常数倍除尽，但不能被其他多项式除尽的多项式称为即约多项式或不可约多项式。

不可约多项式与讨论的域有关，例如 $f(x) = x^2 + 1$ 在实数域上是不可约的，在复数域上可分解为 $f(x) = (x + i)(x - i)$。

定理2-4

设 $p(x)$ 是 $n$ 次不可约多项式，周期为 $m$，序列 $\{a_i\} \in G(p(x))$，则 $\{a_i\}$ 的周期为 $m$。

定理2-5

$n$ 级 LFSR 产生的序列有最大周期 $2^n - 1$ 的必要条件是其特征多项式为不可约的。

流密码

https://vconlln.cn/lfsr.html

作者

Vc0n1ln

发布于

2025-06-24

更新于